SEMANA 1,DÍA 3

          CAMPAÑA DE GRANDES OFERTAS 

1. ¿En cuál de las tiendas obtendrá un menor precio por dicha tablet?
-La tienda super oferta

2. ¿Cuál es el precio que pagaría?
-119,60 soles

3. ¿A qué tanto por ciento equivalen los descuentos sucesivos en “La Económica”?
-58%

4. ¿Cuál es el descuento equivalente a los descuentos sucesivos en “Súper Oferta”?
-60%

Comprendemos el problema:

1.  ¿Cuáles son los datos que se tienen en la situación significativa?  

el precio de la tablet, el descuento y el descuento adicional.

  2. ¿Qué te solicitan determinar en la situación significativa?  

Hallar cual de las tiendas tendrá un menor costo para la tablet   

 3. ¿Qué significa la oferta del 40 % + 30 % con la tarjeta                  Feliz? 

Significa que parte del descuento del 40% que obtiene un 30% con la tarjeta 

    4. ¿Significan lo mismo los descuentos de 40 % + 30 % y 50 % + 20 %? Justifica tu respuesta. 

• Diseñamos o seleccionamos una estrategia o plan  

    1. Explica el procedimiento que seguirías para responder las         preguntas de la situación significativa

 sacar los datos principales como el precio del producto, los %, luego con dichos datos elaborar la regla de tres simples para hallar lo que me piden.

• Ejecutamos la estrategia o plan Reflexionamos sobre el desarrollo

 1. Calcula el descuento que otorga “La Económica” y el  precio con descuento.

           -El descuento es de 58% = 299 x 58 / 100 = 173.42

                                             =299- 173.42= 125.58

     2. Halla el descuento en la tienda “Súper Oferta” y          el  precio de venta.

            -El descuento es de 60% = 299 x 60/100 = 179.4

                                               =299- 179.4 = 119. 60

    3. Responde las dos primeras preguntas de la  situación significativa.

           - pregunta 1:  obtendrá menor precio en la tienda "super oferta"

             pregunta 2: el precio que pagará es 119,60 por ser el más barato.

    4. Determina a qué tanto por ciento equivalen los            descuentos sucesivos en "La Económica".                       Responde la tercera pregunta de la situación                 significativa.

       -pregunta 3: los descuentos de a tienda la economía equivale 58%.

     5. De manera similar, procede con tus cálculos                para responder la cuarta pregunta de la                            situación significativa.

       -pregunta 4: equivale de los descuentos sucesivos en super oferta es 179,4.

Reflexionamos sobre el desarrollo

 1. Si el precio de la tablet hubiera sido otro, ¿qué habría ocurrido con el tanto por ciento equivalente a los descuentos sucesivos? Justifica         tu respuesta.

      -Simplemente los descuentos se hubieran aplicado al precio modificado de             la tablet. Si el precio de la tablet es más alto , Los descuentos serán                    menores, pero aún así el tanto por ciento se aplica en cualquier precio.

SEMANA 2,DÍA 3

                  PROMOCIÓN 2 X 1
 Carla observa en una tienda la promoción de “2x1” en juegos de sábanas. Asimismo, advierte que si tiene la tarjeta de esta tienda, hay un descuento adicional del 20 %. Sabiendo que el precio de lista del juego de sábanas es          129 soles, ¿cuánto pagará Carla por 8 juegos de sábanas?

   A partir de la situación, responda las siguientes preguntas:

 1. ¿La información proporcionada permite dar un solo valor como               respuesta?

     -No, puede dar el valor con descuento y el valor sin el descuento.
  
 2. Describe otro procedimiento que te permita dar respuesta a la                 situación.

   - 8/2= 4 porciones,    4 x s/129 = s/516
            20% de 516 = s/103,20


  con el descuento: s/ 516 - s/ 103,20 = s/ 412,80
   
CARLA PODRIA PAGAR  S/516 0 S/412,80 POR LAS 8 JUEGOS DE  SABANAS.

(día 4)

Situaciones para resolver
 Como parte de un tratamiento, una persona recibió una primera dosis de penicilina de 300 miligramos a las 08:00 horas. A partir de entonces, su cuerpo elimina gradualmente la penicilina, de modo que una hora después solo el 60 % de la cantidad de penicilina inicial permanece activo en su sangre. Esta pauta continúa de tal manera que, al final de cada hora, solo permanece activo el 60 % de la penicilina que tuvo al inicio de esa hora.

1. A partir de la situación, responde:

 a) Elaborar una tabla que muestre la cantidad de penicilina que permanece activa en la sangre de esta persona dos horas después de la aplicación de la primera dosis.

 b)Hallar en qué porcentaje disminuyó la cantidad de penicilina que permanece activa en la sangre de esta persona dos horas después de la aplicación de la primera dosis.

 2. Si el precio de venta de un artículo es de S/ 160, ¿cuál es el precio que se debe pagar luego descontar en forma sucesiva el 15 % y el 25 %?

 a) S/ 105           b) S/ 104            c) S/ 120             d) S/ 100 

3. Margoth tiene un jardín cuya superficie es de forma cuadrada y cada lado mide 2 m. En cierto momento, decide ampliar su jardín de tal manera que la superficie siga siendo de forma cuadrada, pero cada lado mida 4 m. ¿En qué porcentaje se habrá incrementado la nueva superficie del jardín respecto de la anterior?

a) En 75 %         b) En 100 %        c) En 300 %        d) 400 %

 4. Eduardo sufrió una intoxicación y se atendió en una clínica. El seguro médico que tenía asumió el 60 % de todos los gastos que realizó. Si Eduardo tuvo que pagar solo S/ 120, ¿cuál fue el costo total de la atención de Eduardo en la clínica?

 a) S/ 180            b) S/ 200             c) S/ 300              d) S/ 0

SEMANA 3,DÍA 3

                                    LA FERIA 

 22/04/20

 

SEMANA 3,DÍA 4

23/04/20 

                                

                         

                     

SEMANA 4,DÍA 3

29/04/20

a. ¿Cuál es la probabilidad de que la mosca tenga color normal de ojos y tamaño normal de alas?

Número de casos posibles: 140 + 6 + 3 + 151 = 300

Número de casos favorables: 140

140 ∕ 300 ≈ 0,47

La probabilidad es de 0,47% tenga los ojos de color normal y las alas igual.

b. ¿Cuál es la probabilidad de que la mosca tenga ojos bermellón y alas miniatura?

Número de casos posibles: 140 + 6 + 3 + 151 = 300 

 Número de casos favorables: 151

= 151 ∕ 300 ≈ 0,50

la probabilidad de que la mosca tenga ojos bermellón es 0,50%

 c. Si comparamos las dos situaciones anteriores, ¿cuál es más probable que ocurra? 

Comparamos los resultados: 0 ≤ 0,47 < 0,50 ≤ 1

 Comparamos los resultados: 0 ≤ 0,47 < 0,50 ≤ 1 Mientras más próximo esté el valor de la probabilidad a 1, es más probable que ocurra el evento. Por lo tanto, en el experimento de genética, es más probable que la mosca seleccionada tenga ojos de color bermellón y alas miniatura.

1. Si te preguntaran cuál es el suceso más difícil que puede ocurrir, ¿qué responderías sin hacer ningún cálculo? ¿Por qué?

Que la mosca tenga un tamaño normal de alas y sus ojos sean bermellón, porque, para una misma población, le corresponde el menor número de casos posibles.

2. ¿Cuál es la probabilidad de que la mosca de ojos normales tenga alas de tamaño miniatura?

Nº de casos posibles : 140+6+3+151:300Nº de casos favorables: 6p:6/300: 0.02

 3. ¿Qué probabilidad se tiene de que la mosca de alas normales tenga los ojos bermellón?

N° de casos posibles: 140+6+3+151=300
N° de casos favorables: 3
3/300=0,01  

4. ¿Qué conclusión sacarías si la probabilidad hubiera sido 1? ¿Y si fuera 0?

 El primer caso es un suceso seguro, siempre va a ocurrir.

En el segundo caso, el suceso nunca va a ocurrir, es imposible.

En una pequeña ciudad, poblada principalmente por descendientes de los colonos austro alemanes en la selva central, el 40 % de la población tiene cabellos claros; el 25 %, ojos claros, y el 15 %, cabellos y ojos claros. Se escoge una persona al azar:

a. Si tiene cabellos claros, ¿cuál es la probabilidad de que también tenga ojos claros? 

Probabilidad de tener cabellos claros: 40 % = 0,40

Probabilidad de tener ojos claros: 25 % = 0,25 

 Entonces, la probabilidad de que, si tiene cabellos claros, también tenga ojos claros es de 10 %.

b. ¿Cuál es la probabilidad de que no tenga cabellos claros ni ojos claros? 

 Número de casos favorables que no tenga cabellos claros ni ojos claros: 50

Número de casos posibles: 100

 la probabilidad de que no tenga cabellos claros ni ojos claros
 es: 50 ∕ 100 = 1 ∕ 2 = 0,5%

1. ¿Qué diferencia encuentras entre los dos eventos planteados en a y b?

que en el evento "a" definimos la probabilidad de que tengan cabellos claros y a la vez ojos claros y en el evento "b" definimos la probabilidad de que tengan cabellos no claros y a la vez ojos no claros.

SEMANA 5,DÍA 3

6/05/20

Consumo de gas natural en el Perú

 1. ¿De cuántas formas diferentes el grifero puede dar el vuelto a Laura?

 5 x + 2 y = 81 

 5(1) + 2(38) = 81

 5(3) + 2(33) = 81

 5(5) + 2(28) = 81 

5(7) + 2(23) = 81

 5(9) + 2(18) = 81

 5(11) + 2(13) = 81

 5(13) + 2(8) = 81

 5(15) + 2(3) = 81

.:. Entonces hay 8 formas diferentes de darle el vuelto a laura.

2. ¿Qué dato le agregarías a la situación significativa para que el grifero solo tenga una forma posible de dar el

vuelto a Laura? ¿Cuál sería la representación algebraica del nuevo dato?

  

x + y = 39 monedas 

x + y = 36 monedas

 x + y = 33 monedas 

x + y = 30 monedas

 x + y = 27 monedas

 x + y = 24 monedas

 x + y = 21 monedas

 x + y = 18 monedas 

.:. El grifero da de vuelto 39 monedas.

Comprendemos el problema 

1. ¿Qué datos se presentan en la situación significativa? 

Los datos son el importe del gasto en gasolina, del valor del billete con que se pagó y del tipo de monedas que tenía el grifero para dar vuelto.

2. ¿Qué piden hallar las preguntas de la situación significativa? 

  la cantidad de monedas de cada tipo que podría recibir de vuelto, y un dato para que solo exista una forma de dar vuelto.

3. ¿Tienes información suficiente para responder la primera pregunta de la situación significativa? Explica. 

Sí, porque con los datos que se tienen se puede saber la cantidad que va a recibir de vuelto y buscar el número de monedas de cada tipo.

4. ¿Puedes plantear el problema con tus propias palabras? 

 Pagué con un billete de 100 soles para que nos cobren 19 soles y el  grifero se dio cuenta que el vuelto nos lo den con monedas de 2 y 5 soles.

Diseñamos o seleccionamos una estrategia o plan

1. ¿Qué estrategia te ayudará a responder las preguntas de la situación significativa? Argumenta tu respuesta. 

               a) Diagrama de flujo                          b) Plantear una ecuación                   c) Utilizar el ensayo y error

Para la primera pregunta, el ensayo y error, y para la segunda, plantear una ecuación.

2. Describe el procedimiento que realizarías para dar respuesta a las preguntas de la situación significativa. 

Para la primera, ir evaluando el número de monedas de cada tipo que hace un total igual al vuelto. Para la segunda, expresaría una ecuación que relacione los datos, y buscaría el número total de monedas para poder tener otra ecuación. 

Ejecutamos la estrategia o plan

1. Aplica la estrategia elegida y responde la primera pregunta de la situación significativa

Elaborar una tabla y aplicar el ensayo error para completarla. y se tiene 8 casos posibles

2. ¿Qué dato agregarías a la situación significativa para que solo haya una forma posible de dar el vuelto? 

agregar un dato más para  formar una segunda ecuación diferente. En mi opinión seria  que el número de monedas sea 27.

3. Escribe la representación algebraica del nuevo dato y responde la segunda pregunta de la situación significativa

 x + y = 27 (1) 

 2x + 5y = 81 (2)

 Multiplicar la ecuación (1) por –2:

 –2x – 2y = –54 

Resolviendo: y = 9; x = 18 

Reflexionamos sobre el desarrollo

1. ¿Cómo generalizarías tu solución de la primera pregunta de la situación significativa?

Monedas de 5: X

Monedas de 2: Y

Ecuación : 5x + 2y = 81

las formas:

5x + 2y = 81

5(1) + 2(38)=81

5(3) + 2(33)=81

5(5) + 2(28)=81

5(7) + 2(23)=81

5(9) + 2(18)=81

5(11) + 2(13)=81

5(13) + 2(8)=81

5(15) + 2(3)=81

El grifero puede dar el vuelto de 8 formas.

2. Describe otro procedimiento algebraico que puedes emplear para dar respuesta a las preguntas de la situación significativa

Yo elegí el 2do, entonces el dato que le agregue es la cantidad total de monedas usadas por el grifero es 36 monedas

           b5(3) + 2(33)=81

3. Verifica de manera gráfica la solución de la segunda pregunta de la situación significativa. 

Guiándome del segundo dato

La nueva fórmula es :

x + y = 36

5x + 2y = 81

SEMANA 5,DÍA 4

7/05/20

Evaluamos nuestros aprendizajes

1. El director de una institución educativa organizó un proyecto de presentación teatral con sus estudiantes de quinto grado, con la finalidad de reunir fondos y terminar de construir el comedor estudiantil, por lo cual recibió el apoyo de los padres de familia y el de la Municipalidad, que le brindó gratuitamente su anfiteatro.  El costo de las entradas fue de 30 soles para los adultos y 20 soles para los niños. Si el sábado pasado asistieron 248 personas y se reunieron 5930 soles, ¿cuántos adultos y cuántos niños respectivamente asistieron a esa función? 

   a) 151 adultos y 97 niños                                                               b) 124 adultos y 124 niños 

            

   c) 97 adultos y 151 niños                                                               d) 69 adultos y 179 niños

               20x+30y = 5930 soles         

          x+y = 248 personas         

                    20(248-y)+30y = 5930

                    4960-20y +30y = 5930

                    10y = 5930-4960

                     y = 97 adultos     

    

x = 248-97

x = 151 niños

.:. asistieron 97 adultos y 151 niños 

2. Escribe verdadero (V) o falso (F), según corresponda, en cada una de las siguientes proposiciones. 

I. Cuando dos rectas se cortan en un punto, es totalmente seguro que encontramos una solución al sistema de ecuaciones, al cual se denomina sistema compatible determinado. ( V ) 

II. Cuando dos rectas son paralelas en un plano, se encuentran infinitas soluciones al sistema lineal, al cual se denomina sistema indeterminado. ( F ) 

III. En un sistema de ecuaciones lineales, cuando hay más variables que ecuaciones, existe más de una solución. ( V )

  a) V V V                                                 b) V F V 

  c) F F F                                                 d) F V F

5. Un comerciante de algodones de azúcar gana 40 céntimos por cada algodón vendido, pero si no logra venderlo pierde 50 céntimos. Un día en que fabricó 120 algodones, obtuvo una ganancia de 39 soles. ¿Cuántos algodones no logró vender ese día? 

    a) 10 algodones                            b) 7 algodones 

     c) 9 algodones                              d) 12 algodones

             (0.4x) - (0.5Y) = 39.

             0.4(120-Y) - 0.5Y = 39

              48-0.4Y-0.5Y=39

               48-0.9Y=39

                9=0.9Y

                  Y= 10 

  .:. no vendió 10 algodones ese día.

6. En el río Amazonas, un barco recorre 76 kilómetros en 1 hora con la corriente a su favor. De regreso, con la corriente en contra, tarda 4 horas para recorrer la misma distancia. ¿Cuál es la velocidad promedio de la corriente sabiendo que la distancia se calcula con d = v . t (d: distancia, v: rapidez y t: tiempo)?

              a) 47,5 km/h                                     b) 28,5 km/h 

             c) 57 km/h                                         d) 19 km/h

 76 (VB + VR) 1 

 76 = ( 5/3 + VR) 1 

3 x 76 = 5VR + 3 VR x 1

228 = 8 VR 

228/8 = VR 

28,5 km = VR

7. Sergio contrató dos camiones cuyas capacidades de carga son, respectivamente, 3 y 4 toneladas, los cuales hicieron en total 23 viajes para transportar 80 toneladas de varillas de hierro de construcción. Él necesita saber cuántos viajes realizó cada camión para adicionar los gastos por combustible

     Viajes de camión de 3 toneladas : x

     Viajes de camión de 4 toneladas: y  

                 x+y= 23...(i)       3x+4y=80...(ii)  

   despejamos x en (i) : x= 23-y

  reemplazo x en (ii) : 3(23-y) + 4y = 80

                                    69 - 3y +4y =80

                                        x = 11

                                              

 reemplazo y en (i) : X+11 = 23

                                   X=12

10. Un empresario textil de Gamarra desea distribuir un bono de productividad entre sus empleados por su buen desempeño en la semana. Haciendo cálculos, se percata de que si entregara a cada uno 800 soles, le sobrarían 200, y si les diera 900 soles, le faltarían 400. ¿Cuántos empleados hay en su fábrica? ¿Cuánto dinero tiene para repartir? ¿Cómo resolverías el problema sin usar ecuaciones? 

  

       Sumo todo lo que me pide resolver de 800 en 800 y otro con 900 en 900 y sumando el resultado da 5000

   

    1000      500    1

    1800      1400  2

    2600      2300  3

       3400      3200  4

    4200      4100  5 

    5000      5000  6

.:. tiene 6 empleados y 5000 soles para repartir.

SEMANA 6,DÍA 3

13/05/20

                                  La tienda de discos

 “El palacio de los discos” recaudó en una semana 1415 soles por la venta de discos compactos de reguetón y rock. El precio de los CD de reguetón es S/40 y el de los de rock, S/45. Al momento de contabilizar la venta de la semana, la computadora se malogró y se perdió toda la información. La persona encargada solo recuerda que se vendieron 33 discos. Si fueras el encargado de contabilizar las ventas de la semana, ¿cuántos CD de cada género informarías que se vendieron? Grafica en el plano cartesiano. 

• Datos x:
 número de CD de reguetón
 y: número de CD de rock
 Importe en CD de reguetón: 40x
 Importe en CD de rock: 45y

• Planteamos las ecuaciones: {x + y = 33................. (1)

                                                  { 40x + 45y = 1415......... (2)

• Multiplicamos la ecuación (1) por –40:

 {  –40x – 40y = –1320

  {  40x + 45y = 1415

• Reduciendo: 5y = 95 ‒→ y = 19
 • Reemplazamos en la ecuación (1): x + 19 = 33 ‒→ x = 14

Respuesta:

Se vendieron 14 CD de reguetón y 19 de rock. 1.

 1. ¿Qué estrategia se utilizó para resolver la situación significativa? 

Se eligió un sistema de dos ecuaciones con dos incógnitas.

2. ¿En qué consistió el método para resolver el sistema de ecuaciones? ¿Cómo se denomina? 

Se busca que los coeficientes de que una de las variables sean iguales y de signos contrarios para que al sumar salga una incógnita,se llama método de reducción.

3. ¿Qué significan los puntos de cada recta? ¿Cómo interpretas el punto de intersección de ambas rectas? 

 Todos los puntos de una recta se corresponden con todos los pares de valores que cumplen con la ecuación de dicha recta. Entonces, las coordenadas del punto de intersección corresponden a los valores que cumplen simultáneamente con ambas ecuaciones, por lo que afirmamos que representan la solución del sistema de ecuaciones.

SEMANA 6,DÍA 4
14/05/20

Situación 1 

Daniela y sus amigas pagaron 72 soles por 4 empanadas de pollo y 8 refrescos de chicha morada en una cafetería ubicada en un parque; pero la semana anterior consumieron 2 empanadas de pollo y 2 refrescos de chicha morada en el mismo lugar, y la cuenta fue de 26 soles. ¿Cuál es el costo una empanada y un vaso de refresco?

primero sacamos los datos

1.....4x +8y=72

2.....2x+2y=26

ahora reemplazamos 2 en 1

2x+2x+2y+2y+2y+2y=72

52+4y=72

y=5

x=8

.:. El costo de una empanada es de S/ 8 y el vaso de chicha morada, S/ 5.

Situación 2

 Clara sabe que el consumo de frutas en las mañanas y entre comidas es saludable y una vez a la semana se aprovisiona de ellas en la feria de productores más cercana. Ahí encuentra ofertas interesantes como las siguientes: 2 kilos de mango más tres kilos de manzana cuestan 12 soles o 3 kilos de mango más 2 kilos de manzana cuestan 13 soles. Si el precio normal del kilo de mango es 3,50 soles y el precio normal del kilo de manzana es 2, 60 soles. ¿Cuánto de rebaja por kilogramo ofrece la oferta a Clara?

1...... 2x + 3y = 12

2.......3x + 2y = 13

Igualamos las ecuaciones  para obtener el valor de la incógnita y:

12 - 3y/2 = 13 - 2y / 3

36 - 9y = 26 - 4y 

2 = y

Reemplazamos el valor de la incógnita y en la ecuación (1) para obtener el valor de x:

2x + 3y = 12 

2x + 3 (2) = 12 

x = 3

.:. El mango tiene una rebaja de 0.50 y la manzana  de 0.60

situación 3

Juan y Natalia, estudiantes de quinto grado de secundaria, preparan paletas de chocolate con el fin de venderlas y así juntar dinero para su viaje de promoción. La materia prima necesaria para hacer una paleta grande les cuesta 3 soles y, para una paleta chica, 2 soles. Ellos invierten en su proyecto la suma de 50 soles. Con la información dada, responde las siguientes preguntas: 

1. ¿Qué dato le adicionarías a esta situación para que la cantidad de paletas grandes sea igual a la cantidad de paletas chicas?

La cantidad total  de paletas elaboradas es igual a 20.

2. ¿Cuántas paletas serán de cada tamaño?

La cantidad de paletas de cada tamaño sería 10.

3 x + 2  y = 50          

3 (2) + 2 (22) = 50            

3 (4) + 2 (19) = 50            

3 (6) + 2 (16) = 50             

3 (8) + 2 (13) = 50             

3 (10) + 2 (10) = 50           

3 (12) + 2 (7) = 50             

3 (14) + 2 (4) = 50             

3 (16) + 2 (1) = 50 

Situación 4

 En este juego pueden participar una, dos o más personas. Cada jugador de manera personal debe encontrar los números que representan los cuadrados, los triángulos, los círculos, las estrellas y la incógnita, teniendo en cuenta las siete condiciones numéricas del desafío. Gana el juego el primero que logra explicar su solución utilizando sistemas de ecuaciones lineales.

DESAFÍO 1

Reemplazamos el valor de z en la ecuación (1)

2z + 2y = 24
 18+ 2y = 24
  y = 3

Utilizamos los valores de x y z para obtener el valor numérico de la incógnita (¿?):
  x + 3z = ¿?
 5 + (9)3 = ¿?
 32 = ¿?

◻️ = 5        ☆= 3         Δ = 9       O = 7
 ¿? = 32

.:. Los números de las figuras y la incógnita:

DESAFÍO 2

◻️ = X        ☆= Y         Δ =  Z      O= W 


     2x + 2z = 34
x + z + 2x = 31
 2z + x + w = 33
     2x + 2y = 22


  De la ecuación (1) obtenemos:

2x + 2z = 34
 x + z =17


2z + x + w = 33
 20 + 7 + w = 33



2x + 2w = ¿?

14 +12 = ¿?

26 = ¿?


◻️ = 7        ☆= 4         Δ = 10       O = 6
 ¿? = 26 

.:. EL VALOR DE LAS FIGURAS Y DE LA INCÓGNITA.


SEMANA 7,DÍA 3

20/05/20

Accesibilidad física

Una rampa es una superficie inclinada que nos permite conectar dos lugares a diferente altura. Hoy en día, todos los edificios públicos deben contar con acceso para el desplazamiento de las personas con algún problema físico y adultos mayores. La construcción de rampas es obligatoria, siguiendo las especificaciones que indican que su ángulo de inclinación debe tener un rango de 10° a 15° respecto a la horizontal. Actualmente, en el hospital Nueva Esperanza están construyendo una rampa lineal, cuya altura será de 1,5 m al final de ella.

1. ¿Cómo se representa matemáticamente la longitud de la rampa en función del ángulo especificado? 

Datos:

˗ Ángulo de la rampa: Ɵ

˗ Rango del ángulo: 10° ≤ Ɵ ≤ 15°

˗ Altura de la rampa: 1,5 metros

˗ Longitud de la rampa: x

• Representamos la longitud de la rampa usando razones trigonométricas.

y la razón trigonométrica “csc Ɵ”, para calcular la longitud 

= csc Ɵ x = 1,5 ∙ csc Ɵ

.:. La longitud de la rampa en función del ángulo

se expresa como 1,5 ∙ csc Ɵ

2. Representa gráficamente cómo varía la longitud de la rampa.

Comprendemos el problema 

1. ¿Qué ángulo de inclinación debe tener obligatoriamente una rampa? 

Las pendientes variarán en función de la longitud de la rampa; para recorridos iguales o menores a 3 metros, la pendiente será inferior a 10%; para recorridos de 3 a 6 metros, pendiente inferior al 8% y para recorridos de 6 a 9 metros, la pendiente debe de ser igual o menor a 6%






2. ¿Qué altura tiene la construcción de la rampa del hospital Nueva Esperanza?


La altura es de 1,5m.


3. ¿Qué forma geométrica se observa en la imagen lateral de la rampa? Gráfica y escribe sus elementos.

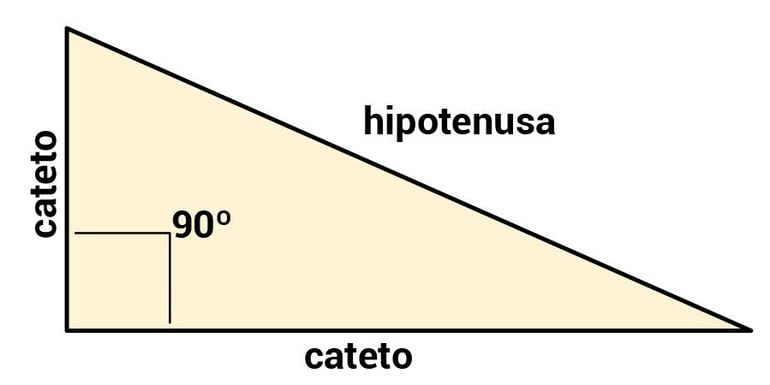
4. ¿Qué razones trigonométricas expresarían una relación entre un ángulo y los lados de la forma geométrica graficada?

coseno y secante.En el triangulo dado, sus lados en relación al angulo son la hipotenusa y el cateto adyacente, por ende, las únicas razones que relacionan el angulo y los dos lados son el coseno-ca/h y secante-h/ca.


5. ¿Qué te piden calcular las preguntas de la situación significativa?

De cuanto sera la longitud de la rampa  

por que al calcular la longitud de la rampa sera mucho mas fácil sacar las demás variables.

Diseñamos o seleccionamos una estrategia o plan.

1. Describe el procedimiento que realizarías para dar respuesta a las preguntas de la situación significativa


Representamos la longitud de la rampa usando razones trigonométricas, debemos encontrar la medida de los tres lados del triangulo rectángulo y sus tres ángulos interiores. Luego Analizaremos cómo varía la longitud de la rampa para diferentes ángulos de elevación.

2. Aplica la razón trigonométrica que relaciona la longitud, altura y ángulo de inclinación de la rampa para representar matemáticamente la longitud de la rampa en función del ángulo especificado.

La razón que usa es seno Osea el cateto opuesto entre la hipotenusa.

3. Responde la primera pregunta de la situación significativa.

x/1,50= csc Ө 

x= 1,5 x csc Ө

.:. Se expresa como 1,5 x csc Ө

4. Completa la tabla




5. Representa gráficamente la variación de la longitud de la rampa

Reflexionamos sobre el desarrollo 

1. Considerando la información registrada en la tabla, ¿qué ocurre con la longitud de la rampa cuando la medida del ángulo de inclinación va aumentando? ¿Por qué?

La longitud depende del ángulo de la rampa de elevación por ejemplo si el ángulo aumenta,menor sera la longitud de la rampa.

2. ¿Qué longitudes de la rampa, según la altura presentada en la situación inicial, cumplen las especificaciones en la construcción de rampas? ¿Por qué? 

longitudes

 x=1,5.csc10° 

  x=1,5.csc 15°  

 cumple con los 10°y 15° obligatorios.

SEMANA 7,DÍA 4

21/05/20

4. Jairo acude con su familia a un centro de esparcimiento de Chosica. Él se sube a un tobogán y desde allí observa un árbol. Para ver la base de este, necesita bajar la vista 37° respecto a la horizontal, y para observar la punta de la copa del árbol, debe levantar su mirada 45° respecto a la horizontal. El tobogán está ubicado a 8 m del árbol. Con esta información, ¿será posible calcular la altura del árbol? Efectúa el procedimiento.

4 k = 8m           

   k= 8m/4      

   k = 2m

Calculamos la altura "h"

 h = 8m + 3k

 h = 8m + 3k (2m)

 h = 14m

.:. Sí es posible y su altura es de 14m.


De acuerdo con las estadísticas, los atropellos son los accidentes de tránsito más frecuentes. A pesar de la responsabilidad del conductor, entre las causas figura el cruce indebido por parte del peatón. Una solución parcial planteada para mejorar la seguridad de las personas es la colocación de puentes peatonales, especialmente en las vías de tránsito rápido. Por ello, se construyó un puente de 7 m de altura; para subir se han acondicionado rampas cuya inclinación es α, y se sabe que Sen α = 0,28. 

Con la información dada, responde las preguntas 5 y 6.

5. ¿Cuáles son los ángulos de inclinación de las rampas mostradas en la imagen?


Sen∝ = 0,28 = 7k/25k
     ∝ = sen 16º
       ∝ = 16º

6. ¿Cuál es la longitud total de las rampas dadas? 

LONGITUD DE LA RAMPA: 

7k + 7k = 7m
      k =0,5m

longitud total : 25k + 25k = 25m


8. Un faro es una torre de señalización luminosa situada cerca de la costa. Se ubica en lugares de paso de las rutas de navegación de los barcos. En su parte superior, dispone de una lámpara potente, cuya luz se utiliza como guía. Juan es el encargado del faro Salaverry, en Barranca, el cual tiene una altura de 70 m. Desde el balcón observa dos barcos situados al este del faro con ángulos de depresión de 60° y 45°. Según la información dada, ¿cuál es la distancia que separa a un barco del otro? 



k√3 = 70

k = 70    √3/3m = 40,4145m


= 40,4145m + x = 70m
= X = 29,59m

.:. La distancia que lo separa es 29,59m.


9. Se observa que dos postes de luz de 360 cm de altura, ubicados a una distancia de 600 cm, iluminan una calle, como lo muestra la figura. Determina la longitud del segmento que queda iluminado por los dos postes.

y + x + z = 600cm

(480cm - x) + x + (480cm - x) = 600cm

x = 360cm = 3,6m

.:. La longitud de los postes es de 3,6m

10. Una asociación que vela por el cuidado ambiental de nuestro litoral contrata una avioneta que sobrevuela las playas más concurridas de Lima para desplegar avisos de difusión. Dos salvavidas, Carla y Miguel, están ubicados en una misma línea recta en la misma dirección, separados por 153 m de distancia. En un determinado momento, entre ellos ven la avioneta, que sobrevuela a una altura constante, con ángulos de elevación de 82° y 53°, respectivamente. ¿A qué altura, aproximadamente, vuela la avioneta? 

VALOR DE "K" :

153m +  4/7k  = 3k 

1071m  4k = 21

  63 = K

Reemplazamos "K"

x = 4k

x = 4 (63) = k

x = 252m

.:. aproximadamente es de 252m

SEMANA 8,DÍA 3

25/05/20

DÍA 4 
28/05/20

Situación 1

 Por la seguridad de su personal y clientes, en una agencia bancaria se instalará una cámara de vídeo en un soporte de pared, de modo que brinde una buena vista de cajeros y usuarios. ¿Cuál es el ángulo de depresión que debe formar la cámara con la horizontal?

.:.Son triángulos iguales entonces "β" es igual a 16.

SITUACIÓN 2

Para la construcción de un nuevo centro comercial de dos niveles, de 6 m de altura cada uno, se están acondicionando dos escaleras mecánicas (subida y bajada). El ingeniero encargado de la obra sugiere que deben tener una pendiente m = 1/√3 como máximo. 


Con la información dada, responde las siguientes preguntas.

 a) ¿Cuál será la longitud de la escalera eléctrica? 




Pendiente = 1/√3
PENDIENTE PARA UN TRIANGULO RECTÁNGULO  = TANGENTE 
1/√3 = 6/x 
x = 6√3
 K = 6

Longitud = 2k

Longitud = 2k = 2 (6) = 12m.

La longitud de la escalera eléctrica es de 12m.

b) Si la altura de cada peldaño es de 200 mm, ¿cuántos peldaños tiene la escalera? 

200 mm = 0,2m

0,2(x) = 6

X = 6/0,2

X = 30 peldaños 

.:.La escalera tiene 30 peldaños.

c) ¿Cuál es el ángulo de elevación de las escaleras con respecto al piso? 

.:.Triangulos iguales entonces "K" vale 6.

Situación 3

 Ante el crecimiento demográfico en una ciudad, numerosas familias recurren a la construcción de sus casas en los cerros, exponiéndose así a muchos peligros. Como paliativo para esta situación, la municipalidad de dicha ciudad ha construido escaleras en diferentes asentamientos humanos ubicados en los cerros, así las personas que viven en esos lugares pueden acceder a sus casas con menos dificultad. Una de aquellas tiene la forma y las dimensiones de la figura. ¿A qué altura se encuentra el final de la escalera?

1) Primer tramo:

x = sen (45º) ·10 m

x = 5√ m

2) Segundo tramo:

y = sen (37º) ·10 m

y = 6 m

3) Tercer tramo:

z =  sen (30º) ·10 m

y = 5 m

Por ende, la altura total será:

H = (5√2 + 6 + 5) m

H = 18.07 m, siendo esta la altura a la que se encuentra la escalera.

X (0,2) = 6 =  RPTA: x = 30

Situación 4

 ¿Qué altura “h” sobre la posición inicial alcanza el columpio cuando gira 45° hacia arriba según la ilustración? Describe tu procedimiento.

K = 2,50/√2 √2/√2 = 2,50√2/2 = 1,25/√2

H = 2,50 – 1,25/√2

RPTA: La altura h que alcanza el columpio es de 0,73 metros.                                                                                                                                                                  

SEMANA 10

DÍA 3     10/06/20

      Empleamos operaciones con números                   racionales en diversas situaciones 

1. ¿Habrá otros valores de temperatura entre las 8 y 10 a. m.? ¿Qué pasaría con el promedio? Propón dos medidas más en el intervalo y observa qué pasa con el promedio. 

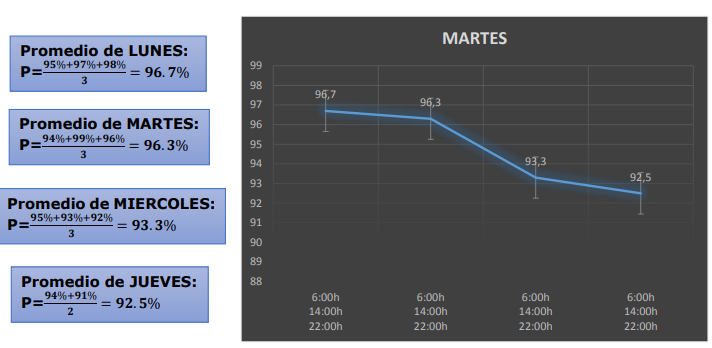
Sí,hay otros valores entre las 8 y 10 a. m. 

.:. Entre esos nuevos valores 29.3 es mayor,entonces la temperatura promedio disminuyo en 29,30 - 28,65 = 0,65ºC 

2. Por lo general, ¿qué esperamos que ocurra con la temperatura entre las 6 a. m. y el mediodía? Para esta situación significativa, propón algunas temperaturas poco probables en el intervalo de 6 a 10 a. m.

La temperatura entre las 6 a. m. es muy baja en todo el día,esperamos que la temperatura aumente.


TEMPERATURAS MENOS PROBABLE:

T(6 a.m) = 28.5 ºC

T(10 a.m) = 21.1 ºC



DÍA 4 
11/06/20

Situación significativa B 

Daniel Ramírez dejó como herencia un terreno de forma rectangular cuyas medidas se muestran en la figura. Su voluntad fue que sea dividido entre sus dos hijos, de manera que cada uno tuviese la mitad. ¿Cuál es el área de terreno que le corresponde a cada hijo si se divide como se muestra en la figura? 

 Datos 
 Dimensiones del terreno: 
 Largo: l = 25,5 m
 Ancho: h = 13 m 
 Área: A = 25,5 × 13 = 331,5 m2
 • Al dividir como se indica, las áreas resultantes serían:
 Largo: l1 = 12,75 m 
 Ancho: h1 = 13 m 
 Área: A1 = l1 × h1 = 165,75 m2 
Respuesta: A cada hijo le corresponde 165,75 m2 del terreno.

1. ¿De qué otra forma sencilla se puede dividir el terreno en dos partes iguales? ¿Cuáles serían sus dimensiones?

Una forma de dividirla es dividiendo el ancho en dos partes iguales: 

                                   A rectángulo = base * altura

                          A rectángulo = 25.5m * 6.5m

                          A rectángulo = 165.75 m2

                          Tenemos 2 rectángulos de 25.5 x 6.5

                                         AΔ = base * altura/2

                                    AΔ = 25.5m * 13m/2 = 165.75m2

                                                   12.75 m                 12.75 m

                                       A = A 12.75x9 + A 12.75x4

                                         A = 12.75 * 9 + 12.75 * 4

                                          A = 114.75 + 51

                                        A = 165.75 m2

7. En la siguiente gráfica, se muestra una autopista que va de norte a sur, en la cual hay un puente peatonal A. Se construyó otro puente B, tal que el puente A está a 600 m al norte del puente B. ¿A la altura de qué kilómetro se encuentra el puente peatonal B? 

A esta al norte de B

B esta al sur de A

Hallamos en que kilometro esta B

Kilometro B = 13.5 km + 600m

Kilometro B = 13.5 km + 600m 1km/ 1000m

Kilometro B = 13.5 km + 0,6 km

Kilometro B = 14.10 km

RPTA: El puente B se encuentra a la altura del km 14.10

8. Se sabe que los metales y otros materiales se dilatan con el calor.

 Una varilla de hierro de 43 cm de longitud ha sido calentada desde 45 °C hasta 90 °C. ¿Cuál es su longitud final?

 Se sabe que la expresión que permite calcular la longitud final debido a la dilatación es:

 L f = L i (1 + α Δt)

Donde:

L f: longitud final

 L i: longitud inicial

 α: coeficiente de dilatación del hierro (α = 1,2 × 10–5 °C–1)

 Δt: temperatura final – temperatura inicial

a) 43,200 22 cm                b) 43,023 22 cm               c) 44,200 22 cm              d) 44,023 22 cm

solución:

 

9. Con los datos del problema anterior, ¿cuál es la longitud final de la varilla de hierro si la temperatura disminuye desde 40 °C hasta 0 °C?

a) 43,020 64 cm                     b) 42,480 36 cm                    c) 42,979 36 cm                     d) 42,999 36 cm

SOLUCIÓN:

10. En una competencia de velocidad, el atleta que va primero ha recorrido 560 m desde el inicio. En ese instante, el último se encuentra a 2/5 de distancia más atrás y el penúltimo está 40 metros por delante del último. Elabora una gráfica en la que señales la distancia que hay entre estos tres atletas.            

560 – 224 = 336m

D = 2/5 (560m) = 224m

UP = 40

U1 = UP + P1 = 224

          40 + P1 = 224

P1 = 224 -40

P1 = 184M

SEMANA 11

DÍA 3

17/06/20

DÍA 4

18/06/20

.:. La respuesta es  4/5 segundos se logra la altura máxima.

2. Al resolver la ecuación identificada en la pregunta 1, se obtiene que el tiempo total que permaneció el balón en el aire es: 

a) 2 segundos                b) 2 /5 segundos              c) 10 segundos                  d) 5 /4 segundos 

El balón permaneció en el aire 4/5 segundos

3.-

.:. el ancho de la franja es de 2m. 

4. La base de una cartulina rectangular mide 8 cm más que su altura. Si le recortáramos 3 cm a su altura, el área de la nueva cartulina sería de 126 cm2 . Calcula las dimensiones de la cartulina inicial.

5. Jairo encuentra el voltaje de un circuito eléctrico utilizando para ello la siguiente ecuación: 

                                                                 x 2 – 2x + 10 = 0

 Sabe que, si la ecuación tiene soluciones reales, el voltaje del circuito es directo; pero si las soluciones son números complejos, es alterno

¿Qué clase de voltaje tiene el circuito diseñado por Jairo?

a) No tiene voltaje        b) Voltaje complejo       c) Voltaje directo           d) Voltaje alterno

.:. el circulo tiene el voltaje alterno.

6.-

.:. El tiempo de vuelo es de 40seg.

SEMANA 14

DÍA 3 

08/07/2020

Resuelvo situaciones que involucran razones trigonométricas de ángulos agudos notables

Una rampa es una superficie inclinada que nos permite conectar dos lugares de diferente altura. Hoy en día, todos los edificios públicos deben contar con acceso para el desplazamiento de las personas con movilidad reducida o adultos mayores. La construcción de rampas es obligatoria, siguiendo las especificaciones que indican que su ángulo de inclinación debe tener un rango de 10° a 15° respecto de la horizontal. Actualmente, en el hospital Nueva Esperanza están construyendo una rampa lineal, cuya altura será de 1,5 m al final de ella.

Si deseamos construir una rampa con un ángulo de inclinación de 15° respecto de la base horizontal, 1. ¿Cuál será la longitud de la rampa tomando en cuenta ese ángulo de inclinación?

Resolución:

• Antes de determinar la longitud de la rampa de  acceso al hospital con un ángulo de 15°, realizo el  cálculo para dos ángulos notables de 45° y 30°.

• Calculo la longitud de la rampa cuando el ángulo es de 45°

1: Representación gráfica de la rampa.

2: Triángulo notable de 45°.

Relaciono las longitudes  de los lados  de ambos triángulos.

Del triángulo 2,  obtengo  el valor de la  constante k: 1,5m =  k

Calculo la  longitud x  de la rampa:  

x = k √2  

x = (1,5 m)(1,41)

x = 2,115 m

• Calculo la longitud de la rampa cuando el ángulo es de 30°

1: Representación gráfica de la rampa.

2: Triángulo notable de 30° y 60°.

Relaciono  las longitudes  de los lados  de ambos  triángulos

Del triángulo 2, obtengo  el valor de la constante k: 1,5 m = K

Calculo la  longitud x  de la rampa:  

x = 2k

x = 2(1,5 m)

x = 3 m

• Ahora calculo la longitud de la rampa cuando el ángulo es de 15°.

1: representación gráfica de la rampa.

2: triángulo notable de 15 y 75°.

Relaciono las longitudes  de los lados de ambos  triángulos.

En 2, calculo el valor  de la constante k:

1,5 m = k (√6 – √2)

1,5 m = k (2,45 – 1,41)

1,5 m = k (1,04)

1,5 m  = k

1,04

1,44 m = k

Calculo la longitud  x de la rampa:

x = 4k

x = 4(1,44 m)

x = 5,76 m

Respuesta: La rampa tiene una longitud aproximada de 5,76 m para un ángulo de 15°.

2. ¿se puede representar de manera matemática esta situación y resolución?

Resolución:

• Represento la situación.

Datos:

˗ Ángulo de la rampa: Ɵ

˗ Rango del ángulo: 10° ≤ Ɵ ≤ 15°

˗ Altura de la rampa: 1,5 metros

˗ Longitud de la rampa: x

• Represento la longitud de la rampa usando razones trigonométricas.

Aplico la regla práctica y la razón trigonométrica “csc Ɵ”, para calcular la longitud de la rampa x:

x = csc Ɵ

1,5

Respuesta: Si, la longitud  de la rampa  en función del  ángulo se expresa  como 1,5 ∙ csc Ɵ.

DÍA 4

09/07/20

Actividad Resolvemos situaciones cotidianas que involucran ángulos de elevación 

Situación 1

1. Las escaleras mecánicas se usan para transportar con comodidad y rápidamente a un gran número de personas entre los pisos de un edificio, especialmente en centros comerciales, aeropuertos, estaciones de transporte público, etc. Para la construcción de un nuevo centro comercial de dos niveles, de 6 m de altura cada uno, se están acondicionando dos escaleras mecánicas (subida y bajada). El ingeniero encargado de la obra sugiere que deben tener una pendiente m como máximo ¿Cuál es la longitud de la escalera eléctrica?

Calculamos la longitud de la escalera con el teorema de Pitágoras:

H 2 = a 2 + c 2

H 2 = (6 m)2 + (6 √3 m)2

H 2 = 36 m2 + 36 ∙ 3 m2

H 2 = 144 m2

H =  √144 m2

H = 12 m

Respuesta: La longitud de la escalera es de 12 m

Si la altura de cada peldaño es de 200 mm, ¿cuántos peldaños tiene la escalera?

• La escalera eléctrica tiene una altura de 6 m, entonces relaciono lo siguiente:

Entre 5              1000mm             ー         1 metro                       entre 5 

            ↪️            200mm                ー       0,20 metros     ↩️

Dividimos la altura donde reposa la escalera entre la altura de cada peldaño.

 6m    =     6.10     =    60 = 30

0,20m     0,20.10        2

Respuesta: La escalera tendrá 30 peldaños.

Situación 2

2.La NASA (National Aeronautics and Space Administration), la agencia del Gobierno estadounidense responsable del programa espacial civil, así como de la investigación aeronáutica y aeroespacial, está a punto de lanzar un cohete de prueba.¿Cuál será la inclinación para iniciar su despegue teniendo en cuenta la siguiente figura?

• Recordamos que el coseno relaciona la medida del lado adyacente y la medida de la hipotenusa:    

                                                     54                       

Cos Ɵ = cateto adyacente            cos Ɵ = 5,4 =  10 =  54 =  3

                Hipotenusa                                   9     9        90     5

                                         

Observamos en el triángulo rectángulo de 37° y 53°:

Respuesta: Por lo tanto, el ángulo de inclinación es 53°.

Situación 3

3. Jairo acude con su familia a un centro de esparcimiento de Chosica. Él se sube a un tobogán y desde allí observa un árbol. Para ver la base de este, necesita bajar la vista 37° respecto de la horizontal, y para observar la punta de la copa del árbol, debe levantar su mirada 45° respecto de la horizontal. El tobogán está ubicado a 8 m del árbol. Con esta información,¿será posible calcular la altura del árbol? Efectúa el procedimiento.

• Represento la situación.

Del gráfico, tengo la siguiente información:

En el rectángulo EBCD, los lados EB = DC = 8 metros. En el triángulo rectángulo AEB, los lados EB = AE = 8 metros, por ser triángulo notable de 45°.

• En el triángulo rectángulo EBD (notable de 37° y 53°) el segmento EB = 4k = 8 m; el segmento ED = 3k.

• Completo los datos y la información obtenida en el gráfico, como se muestra a continuación:

Calculo el valor de k, en el segmento EB:    4k = 8 m

      k = 2 m

Calculo h, la altura del árbol:

H = 8 m + 3k

H = 8 m + 3(2 m)

H = 14 m

Respuesta: Sí, es posible calcular la altura del árbol. Su medida es de 14 m


SEMANA 15
DÍA 3 
15/07/20

Empleamos el ángulo de depresión y utilizamos los triángulos rectángulos en situaciones de la vida cotidiana 

Situación 1

 Por la seguridad de su personal y clientes, en una agencia bancaria se instalará una cámara de vídeo en un soporte de pared, de modo que brinde una buena vista de los cajeros automáticos y sus usuarios. La altura de la cámara al piso es de 2,24m y la distancia desde la pared donde se instalará la cámara hasta el cajero es de 7,68m.

¿Cuál es la medida del ángulo de depresión que debe formar la lente de la cámara con la horizontal? 

Situación 2

 Una empresa construyó un túnel que atraviesa un cerro y conecta dos distritos limeños, tal como se observa en el gráfico. Teniendo como información las medidas obtenidas por los ingenieros. 

DÍA 4

16/07/20

Situación 1

 Juan es el encargado del faro Salaverry, en Barranca, el cual tiene una altura de 70 m. Desde el balcón observa dos barcos alineados en línea recta, con ángulos de depresión de 60° y 45°, respectivamente. 

 ¿Cuál es la distancia, aproximada, que separa a un barco del otro? 

Situación 2

 Para medir la altura de una montaña, un topógrafo realiza dos observaciones de la cima de una montaña con un teodolito que está a 2 metros de altura respecto al nivel del suelo. Desde un primer punto, observa la cima con un ángulo de elevación de 16°. Avanza 750 metros en una línea recta hacia la base de la montaña y desde este nuevo punto, a igual altura que la anterior, mide el ángulo de elevación, que ahora es de 53°. 

¿Cuál es la altura de la montaña?

SEMANA 16

DÍA 3

22/07/20

Situación 1

Hasta el año pasado un décimo de los conductores de vehículos menores excedía la velocidad máxima permitida en avenidas principales. Este año, solo uno de cada cinco conductores lo hace, por lo que podemos decir, que hemos mejorado. Incluso, este último grupo, que representa el 5 % de los conductores, debería regular su velocidad, porque se ha incrementado los pagos por infracción. 

¿Te animas a señalar cuál puede ser el error? ¿Cómo podemos averiguar dónde está el error? 

Debemos tomar medidas drásticas por haber pasado de 10% a 20% y como dice el problema se esta optando como medida preventiva

Situación 2 

En la provincia de Ambo, en la región Huánuco, se seleccionaron tres instituciones educativas a ser candidatas a liderar el proyecto “Escuelas seguras y acogedoras”. 

¿Cuál es la I. E. que tiene mayor porcentaje de varones con respecto a su población total de estudiantes? 

.:. La I.E. Juan José Crespo y Castillo tiene el mayor porcentaje de varones respecto al total de estudiantes.


Situación 3

 La población alemana tienen cada vez más mascotas. Entre los años 2004 y 2005 el número de perros, gatos, pájaros y animales pequeños (sin contar peces ornamentales ni animales de terrario) ha aumentado en 1,3 % hasta llegar a 23,1 millones. La población canina subió 6 % hasta alcanzar 5,3 millones, el número de gatos en 2,7 % hasta llegar a 7,5 millones. En cambio, se constató una reducción en el caso de los pájaros cuyo número disminuyó en 8,7 %, a 4,2 millones. Según las estadísticas, las personas de 40 a 49 años tienen la mayor cantidad de mascotas; estas personas conforman el 25 % de los dueños de animales. El 24 % siguiente en cantidad de mascotas son las personas mayores de 60 años, que se ubican así muy cerca de la punta. 

1. ¿Cuántos pájaros y cuántos perros había entre los años 2004 y 2005 en Alemania? 

2. ¿La situación contiene información suficiente como para calcular el número de animales pequeños en el año 2004? Fundamenta tu respuesta.

 3. Michael dice: “Uno de cada cuatro de los cerca de 80 millones de ciudadanos tiene una mascota, es decir, alrededor de 20 millones”. Cristina piensa que esta afirmación es errada. Encuentra argumentos en pro de Cristina. De ser el caso, explica el problema aplicado a un ejemplo que tú elijas. 

Situación 4 

En la tienda A ofrecen un descuento del 20 % por la compra de un vestido cuyo precio es 100 soles. Si luego a ese mismo vestido le dan otro descuento sobre el que ya se dio del 25 %, ¿cuál es el precio final de dicho vestido? 

.:.El precio final del vestido es S/ 60.

DÍA 4

23/07/20

Situación 1

 Jesús y Alessandra, desean hacer un regalo a sus abuelos por Fiestas Patrias, para lo cual visitaron distintos centros comerciales donde venden artículos o herramientas de carpintería. En uno de ellos, observaron que una caja de herramientas les costaba 150 soles. Al no contar con ese monto, decidieron volver la primera semana de julio, después de juntar sus ahorros. Pero se dieron cuenta que el precio se había incrementado en un 10 %. Al faltarles dinero, decidieron volver la siguiente semana, en la que observan que el precio de la caja de herramientas se había incrementado en un 20 % del precio que observaron en la primera semana de julio. Ellos cuentan con un billete de 200 soles. 

Jesús dice: “el precio se ha incrementado en 30 % del precio inicial pero nos alcanza y nos sobra cinco soles. A lo que Alessandra dice: “no se ha incrementado en 30 %, pero sí nos sobrarían dos soles”

Jesús dice: “el precio se ha incrementado en 30 % del precio inicial pero nos alcanza y nos sobra cinco soles. A lo que Alessandra dice: “no se ha incrementado en 30 %, pero sí nos sobrarían dos soles”

1. Determina el aumento único que equivale a dichos aumentos sobre el precio inicial de la caja de herramientas. ¿Quién de los dos tiene razón? 

.:.El aumento único es 32%. Alessandra tiene razón, ya que ellos poseían 200 y soles, y al comprarlo les sobraría 2 soles de vuelto.


Situación 2

Miguel es un joven de 25 años que ha terminado sus estudios universitarios y ha empezado a trabajar hace seis meses. Él está muy contento puesto que está trabajando en la industria textil igual que su padre y algo que siempre le llamó la atención estrabajar desarrollando una experiencia en el usuario única e insustituible. Producto de su trabajo él ha decidido guardar parte de su dinero y como su abuelito Gonzalo siempre le recomendó, ha decidido ahorrar el 50 % de su gratificación, para ello, ha

visitado 4 instituciones financieras y le han dado las siguientes alternativas

1. ¿En qué institución financiera le conviene a Miguel empezar a ahorrar tomando en cuenta que necesitará usar dicho dinero dentro de cuatro meses? Su gratificación ha sido de S/ 2000. 

.:. a miguel le conviene la financiera D


SEMANA 18
DÍA 3
05/08/20

Determinamos el tipo de variable y muestra en diversas situaciones y calculamos la media aritmética

Situación 1
Se desea obtener la estatura promedio de los estudiantes del quinto grado de Educación Secundaria en instituciones educativas pertenecientes a la UGEL (Unidad de Gestión Educativa) N.° 08 Cañete como un indicador anual de su desempeño físico. 

Determina:
 (a)la población
(b)muestra
(c)variable en estudio
(d)tipo de variable.

Respuesta al ítem a:
La población son los y las estudiantes del quinto grado de Educación Secundaria de las instituciones educativas que pertenecen a la UGEL N.°08 Cañete.

Respuesta al ítem b:
La muestra probabilística se obtendría por un muestro aleatorio simple, dado que todos los estudiantes del quinto grado de Educación Secundaria de la UGEL N.°08 están en las condiciones de ser elegidos para medir su estatura.

Respuesta al ítem c:
Como se desea obtener la estatura promedio de los y las estudiantes que componen la población, la variable a investigar es su estatura en metros.

Respuesta al ítem d:
El tipo de variable es variable cuantitativa, porque resulta de una medición, sus valores son cantidades, números y pueden ser decimales, entonces es una variable cuantitativa continua.

Situación 2

Se desea aplicar una nueva técnica de enseñanza a estudiantes del nivel Secundaria en un distrito de Pisco en Ica. Motivo por el cual, se aplicará un examen a un grupo de adolescentes del distrito. Todos los estudiantes que cursan el tercer grado han sido escogidos para recibir una nueva técnica de enseñanza en una I. E. del distrito de Pisco. El examen debe ser administrado antes y después de ser aplicada la técnica. Determina la población, muestra, variable en estudio y tipo de variable.

Determina:
(a)la población
(b)muestra
(c)variable en estudio
(d)tipo de variable.

Respuesta al ítem a:
La población son todos los estudiantes del tercer grado del nivel Secundaria de Ica.

Respuesta al ítem b:
La muestra es una I. E. del distrito Pisco, ha sido escogida al azar, lo que significa que es muestreo aleatorio simple.

Respuesta al ítem c:
Con respecto a las variables a estudiar son los resultados antes de ser administrada la técnica y los resultados después de haber sido aplicada la técnica.

Respuesta al ítem d:
El tipo de variable que se visualiza es, en ambos casos, una variable cualitativa ordinal dado que habrá una jerarquía en los resultados, AD, A, B y C.

Situación 3

En la ciudad de Trujillo, en el Concurso Nacional de Marinera se pide a los concursantes la siguiente información: sexo, mes de nacimiento, edad, estatura para ubicarlos según categorías. El profesor de una academia de marinera solicita a sus estudiantes dichos datos, los cuales registra en la siguiente tabla: 

Identifica y clasifica las variables.

variables:                    clasificación:

sexo:                         cualitativa nominal            

mes de nacimiento    cualitativa nominal

edad:                         cuantitativa y cuantitativa discreta

estatura y peso:       cuantitativas continuas

Situación 4

 Se han tomado varias muestras de cierto tipo de queso y se ha determinado su cantidad de proteína por cada 100 gramos. Hemos encontrado la siguiente información: 26,5; 24,8; 25,3; 30,5 y 21,4. Determina la cantidad promedio de proteína encontrada en la muestra por cada 100 gramos de queso que se elabora.

.:.El promedio o media aritmética de proteína en el queso es de 25,7g por cada 100g de queso.

Situación 5

Deseamos determinar la edad promedio de los estudiantes de una escuela técnica de nivel superior al iniciar sus estudios. Supón que se toman las edades de algunos de los estudiantes de cierta clase y son las que siguen: 20; 18; 18; 19; 18; 19; 35; 20; 18; 18 y 19

.:. El promedio o media aritmética de los estudiantes de esta escuela de nivel superior es 20,18 años al iniciar sus estudios.

Situación 6 

Se tiene información proveniente de dos muestras que nos hablan del número de hijos y del número de familias de dos comunidades de la diversidad de nuestra Amazonía: los Kichwas y los Shipibo-Konibo.

 • Estas dos comunidades se caracterizan por tener un espíritu emprendedor. Tienen los mismos derechos y oportunidades que otros comerciantes de la región.

 • Marco, presenta la propuesta al gobierno regional para la inclusión de las comunidades en las ferias regionales para la venta de sus productos. Para el sustento incluirá los datos del número de hijos de estas familias. Para ello, es importante colocar el valor más representativo con respecto al número de hijos de las dos comunidades. ¿Cuál es el valor de la media para cada una de las muestras de las comunidades? Si desea que los datos sean los más homogéneos, es decir, los más cercanos a la media, ¿cuál sería este valor y de qué comunidad sería?

.:. El promedio o media aritmética para los “kichwas” será de 3 hijos por familia.

 .:.Tanto los “kichwas” como para los “shipibo-konibo” el promedio de hijos que se tiene por familia es de 3, a pesar de que las muestras tienen diferente cantidad de familias.

DÍA 4

06/08/20

Representamos los datos en una tabla de frecuencias y lo expresamos en un gráfico estadístico 

Situación 1 

Se tiene el número de hijos de las familias de dos comunidades shipibo-konibo y kichwas: 

a) Representa los datos en una tabla de frecuencias. 

cantidad de hijos en la comunidad kichwa:

cantidad de hijos en la comunidad shipibo-konibo

b) Expresa mediante un gráfico estadístico la cantidad de hijos que tienen las familias de las comunidades shipibo-konibo y kichwas. 

GRÁFICO DE FRECUENCIA DE LA COMUNIDAD KICHWA:

GRAFICO DE FRECUENCIA DE LA COMUNIDAD SHIPIBO-KONIBO:

Situación 2 

El horario de llegada denota un orden o secuencialidad, por lo tanto, es una variable ordinal, entonces, supongamos que clasificamos a la cantidad de personas que llegan a atenderse en un hospital de Lima Metropolitana entre las 09:00 h y el mediodía. A partir de ello, tenemos el siguiente cuadro:

Representa mediante un gráfco los datos señalados.

Planteo el siguiente gráfico utilizando relojes:

 En el horario de 09:00 h hay 9 relojes que representan a las 45 personas que han llegado en ese horario. Por lo tanto, cada reloj representa a 5 personas, ya que 9por 5es igual a 45. Elijo que cada reloj equivalga a 5, porque los datos de la cantidad de personas en cada hora son múltiplos de 5. Por ejemplo: 45, es múltiplo de 5. De igual manera 35, 20 y 15 todos son múltiplos de 5. Por ello, la cantidad de relojes en el pictograma representa a la cantidad de personas que llegó en ese horario en grupos de 5.

SEMANA 19

DÍA 3

12/08/20

Nos relacionamos desde nuestra diversidad

A partir de la situación, responde el siguiente reto (puedes responder de manera escrita u oral, grabando un audio). 

• ¿Cuál es el valor más representativo del conjunto de datos para la variable en estudio?

Calculo la media aritmética de los datos de la comunidad Kichwa.
X = (1 x 3) + (2 x 4) + (3 x 6) + (4 x 4) + (5 x 3)/20
X = 60/20 = 3

Rpta: la media aritmética de los datos de la comunidad Kichwa es 3.
Calculo la media aritmética de los datos de la comunidad Shipibo-Konibo
X = (1 x 6) + (2 x 3) + (3 x 2) + (4 x 3) + (5 x 6)/20
X = 60/20 = 3

Rpta: la media aritmética de los datos de la comunidad Shipibo-Konibo es 3.

Me = x10 + x11/2 = 3 + 3/2 = 6/2
Me = 3

Rpta: La mediana de la comunidad Kichwa será de 3 hijos por familia.

Me = x10 + x11/2 = 3 + 3/2 = 6/2

Me = 3

Rpta: La mediana de la comunidad Shipibo-Konibo será de 3 hijos por familia.

Mo = 3

Rpta: La moda de la comunidad Kichwa será de 3 hijos por familia.

Mo1 = 1 y Mo2 = 5

Hay 2 modas entonces la muestra es bimodal.

Rpta: La moda de la comunidad Shipibo-Konibo será de 1 y 5 hijos por familia.

DÍA 4

13/08/20 

Determinamos e interpretamos las medidas de dispersión para tomar decisiones

 Determina la comunidad que participará en la feria regional, teniendo en cuenta que sus datos estadísticos sean los más homogéneos. 

Calculo la varianza de los datos de ambas comunidades 

Tabla de frecuencia de la cantidad de hijos en la comunidad kichwa.

la varianza en la comunidad kichwa es 1,6


Tabla de frecuencia de la cantidad de hijos en la comunidad Shipibo - konibo 

la varianza en la comunidad de shipibo - konibo es 2,7

Entonces la comunidad kichwa al tener una menor desviación,sus datos se encuentran  más concentrados hacia el 3,que es la media aritmética,que la comunidad Shipibo - konibo. 

calculo la coeficiente de variacion de ambas comunidades 

SEMANA 20

DÍA 3

19/08/20

Procuramos nuestro bienestar emocional con prácticas de vida saludables

 ¿Cómo podríamos saber si nuestro índice de masa corporal (IMC) y el de nuestros familiares están dentro del rango normal? 

Tendríamos que aplicarla formula del IMC:
IMC = MASA (KG) 

        (ALTURA (M)) ² 

Así podríamos determinar el índice de masa corporal de mis familiares y comprobar si están dentro del rango normal o no.

• ¿Qué dieta nutritiva debemos consumir de acuerdo con nuestro IMC?

Las frutas, las verduras, los cereales integrales, la leche y los productos lácteos sin grasa o bajos en grasa.
Poca cantidad de grasas saturadas, grasas trans colesterol, sal (sodio) y azúcares adicionales. Carnes magras, aves, pescado, frijoles, huevos y nueces

DÍA 4

20/08/20

Determinamos el interés compuesto a partir de ahorros y créditos para promover el emprendimiento en actividades físicas

Situación 1 

 En la I. E. Nuestra Señora de las Mercedes de Huánuco, la comunidad educativa ha considerado trabajar el eje articulador “Vida saludable”. En tal sentido, se ha solicitado a cada uno de los estudiantes que calculen el IMC de todos los integrantes de su familia. Los datos registrados por Marcelo son los que se muestran en la tabla:

a. Los datos de la tabla redondeando todos los valores del IMC hasta los décimos. 

b. Identifica cuál es la condición de salud de cada integrante de la familia, según su estado asociado a los valores del IMC en la tabla.

c. ¿Cuántos kilogramos debe bajar, como mínimo, Marco para que su peso sea normal?

Masa corporal (marco)= (24,9) (3,0625)= 76,25625 ≈ 76,3
                                         
                                            78,5 kg - 76,3 = 2,2 kg.

 Rpta: Para que marco tenga su masa corporal normal, debe bajar aproximadamente 2,2 kg, 

Situación 2 
El papá de Karina es profesor de educación física y, actualmente, administra un gimnasio. El gimnasio se mantiene cerrado de acuerdo con las normas sanitarias. Con la finalidad de cubrir los costos y poder reflotar el establecimiento, solicitó un préstamo de S/ 100 000, para ser pagado en 5 años, con una tasa de interés anual del 10 %. Karina realizó sus cálculos y está preocupada porque cree que su papá se equivocó al decir que devolverá un monto equivalente a S/ 161 051 y no S/ 150 000 que ella calculó. ¿Cómo podemos ayudar a Karina y a su papá a salir de dudas? Justifica tu respuesta.

Datos: 
𝐶0 = S/ 100 000 (préstamo) 
t = 5 años
 r = 10 % = 0,1 
M = ? 
Solución:
 𝑀 = 𝐶0 1 + 𝑟 ∙ 𝑡 
𝑀 = 100 000 1 + 0,1 ∙ 5 𝑀 = 100 000 1,5 
𝑀 = 150 000 El monto a devolver sería de S/ 150 000. 
Rpta: Con este resultado puedo verificar que Karina interpretó mal el problema y aplicó la fórmula del interés simple.

Situación 3 
Según el INEI el 35,5 % de personas de 15 a más años, en nuestro país presenta sobrepeso, que es un factor de riesgo para diversas enfermedades. Para ponerlo en marcha, ni bien sea superada la emergencia sanitaria, un grupo de jóvenes en coordinación con la municipalidad de su distrito, proyectan un centro recreacional para la práctica de deportes y diversas actividades físicas. Para tal efecto, acuden a una Caja Municipal y solicitan un crédito de S/ 12 000 para ser pagado en 3 años. La entidad financiera les aprueba el crédito, aplicando una tasa de interés del 3,5 %, capitalizable mensualmente. ¿Cuál es el monto de dinero que deberán devolver los jóvenes al cabo de los 3 años?

Datos: 
𝐶0 = S/12 000 
t = 3 años 
r = 3,5 % = 0,035 (capitalizable mensualmente) 
n = 12 (número de periodos en un año) 
M = 𝐶𝑓 =? 
Solucion:
 M = 𝑪𝟎 𝟏 + 𝒓 𝒏 𝒏 ∙𝒕
 M = 12 000 1 + 0,035 12 12 ∙3
 M = 12 000 1 + 0,00291666 … 36 
M = 12 000 1,002917 36 
M = 12 000 1, 1105
 M = 13 326
 Rpta: El monto que deberán devolver los jóvenes a la caja municipal al cabo de tres años es de S/ 13 326, aproximadamente. 

Situación 4
 Julio observa en un diario la siguiente tabla:

Julio termina sus estudios en 3 años y ya tiene reunidos S/ 8 000. Con ese dinero proyecta abrir una tienda de implementos deportivos apenas termine sus estudios. ¿En qué entidad financiera deberá depositar Julio su dinero mientras estudia, para obtener la mayor cantidad de dinero? ¿Qué capital dispondrá para su proyecto al cabo de los 3 años?

co=8000

r (interés)=4,2% --=0,042

t= 3 años

M= ?

M=Co(1+r.t)

M= 8000 (1 + 0,042 . 3)

M=8000(1 + 0,126)

M=8000(1,126)

M= 9 008

Rpta: debe de depositar  su dinero en "oriente" ya que el interés que le darán es mayor comparado con los otros y al cabo de 3 años  dispondrá de S/ 9 008




SEMANA 21

DÍA 3

26/08/20

Situación 1
Luis planea ahorrar en un banco S/ 10 000 para generar ganancias y emprender un negocio. Buscó información en las páginas web de varias entidades financieras y seleccionó dos bancos que ofrecen las siguientes tasas de interés si el depósito es a plazo fijo por 3 años:

• ¿En cuál de los bancos obtendrá un mayor interés por su dinero? ¿Cuál es el interés? 
Por su dinero obtendrá un mayor interés en la financiera "El emprendedor"  
El interes será S/1910,16
• ¿Le conviene a Luis ahorrar su dinero en una entidad financiera si desea emprender un negocio con las ganancias? 
Si la cuenta de ahorro es plazo fijo,si le conviene cuando no necesite el dinero,en esos 3 años,ya que podría perder el beneficio. 

Situación 2

 Pago del IGV y del ITF
 • ¿Cuánto debe ser el depósito de dinero incluyendo el IGV y el ITF?

DÍA 4

27/08/20

Situación 1
 Juan proyecta alquilar un local para hacer funcionar un gimnasio cuando las normas sanitarias lo permitan. El alquiler mensual es de S/ 2000, ¿a cuánto equivale el impuesto que debe pagar el dueño por alquilar su local?

Rpta: El impuesto que debe pagar el dueño por el alquiler del colar es de S/100 (mensual).

 Situación 2
 Alexis Gonzales tiene 3 locales en alquiler. El pago del alquiler es mensual, el primer local, lo alquila para un negocio de frutas a S/ 800; el segundo, para vivienda a S/ 1200 y, el tercero, es una oficina, en el centro de la ciudad, a S/ 1500. ¿Cuánto debe pagar por impuesto a la renta anual?

Rpta: Por IR anual debe pagar S/2 100.

 Situación 3
 Una persona pone a la venta su vivienda en S/ 420 000, la misma que se habilitará para hacer funcionar el gimnasio. ¿Cuánto deberá pagar cómo impuesto a la renta por la venta del mencionado inmueble?

Rpta: Deberá pagar   S/21 000 al mes.

Situación 4
Un preparador físico emite un recibo por honorarios por la suma de S/ 3600 por preparar físicamente a los integrantes del equipo que participará en el campeonato de fútbol organizado por la municipalidad. ¿Cuál será la retención que deberá hacer la directiva del club y el monto neto a recibir?

Rpta: La retención que deberá hacer la directiva del club es 288 soles, y el monto neto a recibir es de S/3 312.

 Situación 5
 El profesor Pedro va a emitir un recibo por honorarios por la suma de S/ 3000 por el dictado de clases por horas en una universidad, ¿cuál será el monto de retención y el monto neto para recibir? Situación 6 La empresa “Constructores” dispone de S/ 4784 para el pago neto por los servicios de un ingeniero obras. ¿Cuál será el monto de pago del ingeniero?

Rpta: El monto de retención es 240 soles, y el monto neto a recibir es de S/2 760.

Situación 6
La empresa “Constructores” dispone de S/ 4784 para el pago neto por los servicios de un ingeniero obras. ¿Cuál será el monto de pago del ingeniero?

Rpta: El monto de pago del ingeniero es de S/5 200.


SEMANA 22
DÍA 3

02/09/20


• ¿De qué manera podríamos saber cuáles son los efectos que ocasionan los sismos en un determinado lugar, conociendo su epicentro

A través de reemplazar los valores de las coordenadas del centro y radio a través de la siguiente manera:

(x-h)²+(y-k)²=r²

Donde h es la que se encuentra en las coordenadas de la "x" y k en el de "y".

Además debemos de saber su radio.

 • ¿Qué características deberían tener los proyectos de inversión para la construcción de obras que permitan utilizar los recursos de manera responsable? 

de obras que permitan utilizar los recursos de manera responsable?

Deberían ser económicos y regular el material en uso, que no sea contaminante y no perjudique el bienestar de todos.

• ¿Qué beneficios trae a la población el consumo responsable de los recursos?
Obtenemos un ahorro económico, disfrutamos de la biodiversidad y generamos igualdad social.

¿De q

DÍA 4
03/09/20

Situación 1 
El Instituto Geofísico del Perú (IGP) informó que el último sismo registrado en la región Arequipa tuvo una magnitud de 4 grados en la escala de Richter. Según el reporte de dicho instituto, el epicentro se localizó a 4,2 km este y 3,8 km sur del centro de la ciudad de Camaná. Además, se sabe que alcanzó una profundidad de 20 kilómetros con un radio de 4,5 km a la redonda. ¿Dicho sismo afectó a la ciudad de Camaná?


Si el sismo tiene un alcance de 4,5km a la redonda y tuvo su epicentro a 4,2km al este y 3,8km al sur del centro de Camaná, la distancia a la ciudad del epicentro es:

El sismo no afecta a la ciudad de Camaná

Situación 2
El servicio sismológico de Baja California detectó un sismo con origen en la ciudad de Mexicali a 5 km este y 3 km sur del centro de la ciudad, con un radio de 4 km a la redonda. ¿Cuál es la ecuación de la circunferencia del área afectada? ¿Afectó el centro de la ciudad de Mexicali?

Situación 3 
En el departamento de Arequipa, se ha registrado un sismo que tuvo una magnitud de 5 grados en la escala de Richter, según el reporte del Instituto Geofísico del Perú, el epicentro se ubicó a 10 km al este y 6 km al sur del centro de la provincia de Caravelí. Además, se sabe que alcanzó una profundidad de 20 km con un radio de 30 km. Un cable de alta tensión cae exactamente en el límite norte de la zona afectada y paralela al eje X del efecto de las ondas sísmicas. 

a. ¿Cuál es la ecuación de la circunferencia que nos permitirá determinar el límite del efecto de las ondas sísmicas?
 b. ¿Cuál es el límite máximo ubicado al norte y paralelo al eje X del efecto de las ondas sísmicas donde cae el cable de alta tensión?

Situación 4

La plaza Bolognesi ubicada a 5 km al sur y 3 km al oeste del centro de Lima tiene un diámetro de 0,1 km, aproximadamente. Si ocurriera un sismo 7 grados en la escala de Richter, siendo allí el epicentro, y un poste de luz se derrumba sobre el borde ubicado en el extremo superior de la plaza.
a. ¿Cuál sería la ubicación donde cae el poste?
 b. ¿Cuál sería la ecuación de la recta que representa el poste? 
c. Si el epicentro se ubicaría en la zona norte, interceptando en el extremo superior y tendría un diámetro de 0,2 km, ¿cuál sería la ecuación de la circunferencia que se generaría?

Situación 5
 En la municipalidad de una provincia del país, el alcalde proyecta construir un puente de 20 metros de largo por 3 metros de ancho, una construcción que el pueblo necesita y debe servir por muchos años. Le han recomendado utilizar cilindros congruentes, de alta duración. Al buscar información, encuentra que la altura de los cilindros es de 3 metros y solo cuenta con la información de la ecuación de la base de cada cilindro: x2 + y2 – 2x – 2y – 2 = 0. ¿Cuántos cilindros debe el alcalde autorizar comprar al ingeniero encargado de construir el puente?

Si los cilindros se colocan en forma horizontal y todos paralelos uno al lado del otro, se necesitan 5 de ellos para construir el puente.

 Cada cilindro tiene 2 metros de radio, es decir 4 metros de diámetro. Si colocará los cilindros en forma horizontal y perpendicular al puente para apoyar sobre ellos la calzada va a necesitar 5 cilindros para cubrir los 20 metros de distancia.

SEMANA 23

DÍA 3

09/09/20

Situación 1

 El puente Perené 
El puente colgante Perené, tiene capacidad para soportar el tránsito de vehículos de hasta 45 toneladas, facilitando así el comercio de mercadería proveniente de la comunidad nativa de Capachari con el distrito Pichanaqui. Se sabe que el puntal más corto mide 5 m. 

• ¿Cuál será la altura donde está ubicado el cable a 32 m del pilar?

Situación 2 

En el siguiente gráfico se muestra un puente construido por una municipalidad sobre una estructura con formas parabólicas congruentes, que fueron evaluadas respecto a su resistencia sísmica. El punto (6; 0) es de tangencia y la ecuación de la parábola de la izquierda es x2 = −4y.
¿Cuál es la ecuación de la parábola de la derecha?

DÍA 4

10/09/20

Situación 1
 El parque zonal Huayna Cápac El parque zonal Huayna Cápac cuenta con amplias áreas verdes, donde se puede disfrutar de un buen paseo con toda la familia. Se sabe que uno de los accesos del ingreso principal al parque está formado por dos partes, la parte inferior que mide 2 m de altura y 4 m de ancho y la parte superior de forma parabólica que mide 2 m de altura y 4 m de ancho. • ¿Cuál será la ecuación que represente el acceso del ingreso principal? 

Situación 2
Un municipio está a punto de inaugurar un túnel cuyo arco parabólico tiene las siguientes dimensiones, 18 m de altura y 24 m de base. Se desea colocar un reflector de mayor intensidad luminosa en la parte alta del túnel que está ubicado a 8 m hacia la derecha de la base del centro del arco parabólico. ¿A qué altura del túnel se ubicará dicho reflector? 

Situación 3 
Colaborando para mejorar mi comunidad Un grupo de estudiantes presenta a las autoridades del distrito un proyecto orientado a la construcción en la plaza de armas de una laguna artificial en forma circular con un radio de 5 m y sobre ella un arco parabólico, en el cual se pondrá el nombre del distrito en su punto máximo. Las autoridades del distrito ordenan la ejecución de dicho proyecto, el mismo que estará ubicado exactamente 12 m al este y 18 m al sur de la municipalidad y el arco parabólico se ubicará entre los extremos sur y norte de la laguna artificial y tendrá una altura de 10 m.

 a. Calcula la ecuación general de la circunferencia. 

b. Calcula la ecuación general de la parábola.

Situación 4 
Uniendo nuestras comunidades Hace algunos años atrás, los habitantes de dos distritos tenían serios problemas para comunicarse, e incluso tener acceso a productos de primera necesidad les resultaba complicado. Esto llegó a su fin cuando se construyó un túnel de forma parabólica, el cual presenta como altura máxima 4 m de altura y tiene un ancho máximo de 12 m, facilitando así la mejor convivencia entre las personas. Si el túnel tiene la forma de una parábola, calcular su ecuación general.

SEMANA 24

DÍA 3

16/09/20

Empleamos diversos métodos de solución para resolver problemas sobre ecuaciones

A partir de la situación, responde lo siguiente y resuelve las situaciones:
 • ¿De qué manera podríamos calcular los presupuestos para el mantenimiento y preservación del área verde?

Restando el desembolso mensual, los pagos fijos y de reserva.

 • ¿Cómo aplicarías las ecuaciones e inecuaciones frente a la situación de contexto planteada? 

Identificando primero aquellas acciones que dependen de una variable, para luego resolver.

• ¿Qué beneficios produce contar con un área verde en una comunidad conciliadora?
   Mejoran el bienestar emocional.

        Mejora la salud física.

         Fomentan la vida al aire libre y el encuentro social

          Aumenta la conciencia ambiental de los ciudada

Situación 1

 Distribuyendo nuestros gastos mensuales La administración del área verde cambia cada dos años y el presupuesto que será desembolsado por el Ministerio del Ambiente con la finalidad garantizar su mantenimiento y preservación, es S/ 5400 mensuales, empezando la entrega del dinero el mes de abril. Uno de los distritos encargados de la administración decide elaborar su presupuesto de gastos mensuales: agua, S/ 320; luz, S/ 480; mantenimiento, S/ 600; preservación, S/ 400 y fondo de contingencia, S/ 200. Sabiendo que el monto destinado al pago de agua y luz son gastos fijos, además, cada mes se debe brindar el servicio de mantenimiento el triple de veces que se brinda el servicio de preservación.

Elaborando el presupuesto mensual según  los datos proporcionados:

Agua:                                                 S/320

Luz                                                     S/480

Mantenimiento:                                S/600

Preservación:                                   S/400

Fondo de contingencia:                   S/200

Para mantenimiento y preservación, quedara asignado:

5400 – 320 – 480 – 200 = S/4400.

Se sabe que por cada servicio de mantenimiento y preservación es:

                                           Nº de veces:

Mantenimiento:              S/600                    3x = 6

Preservación:                  S/400                    x = 2

Planteando:

3x (600) + x (400) = 4400                                                  Mantenimiento = 600.6 = S/3600

 1800x + 400x = 4400                                                         Preservación = 400.2 = S/800

                X = 2

1. ¿De qué manera podríamos calcular el presupuesto para mantenimiento y preservación? 

5400 – 320 – 480 – 200 = S/4400.

2. ¿Cuántas veces durante el mes pudieron realizar el servicio de mantenimiento? 

Se pudieron realizar 6 veces.

3. ¿Cuántas veces durante el mes pudieron realizar el servicio de preservación? 

Se pudieron realizar 2 veces.

4. ¿Cuánto dinero tienen ahorrado como fondo de contingencia al mes de diciembre? 

Desde abril  hasta antes de diciembre, se tendría ahorrado como fondo de contingencia lo concerniente a 8 meses. Esto es 8 x 200 = S/1600

5. En el mes de diciembre solo les asignaron S/ 2500, debiendo utilizar su fondo de contingencia y además realizar tres servicios de mantenimiento y tres servicios de preservación. ¿Cuál fue y cómo se obtiene el saldo en dicho mes?

Se tendrá de presupuesto para este mes de diciembre: S/2500 + S/1600 = S/4100

Agua:                                                S/320

Luz                                                   S/480

Mantenimiento:                               S/600 x 3 = 1800 -  ---  -   - Gasto total, sin considerar el fondo de  Preservación:                                   S/400 x 3 = 1200 - ---  -   --     -  contingencia: = S/3800

                                            

Fondo de contingencia: S/200

Saldo = S/ 4100 – S/3800 = S/300

DÍA 4

17/09/20

Aplicamos la ecuación cuadrática en la resolución de diversas situaciones 

Situación 1

 Se tiene un terreno rectangular. Al averiguar sus dimensiones, se nos informó que el lado más corto se diferencia del lado más largo en 2 m y su área es de 48 m2. ¿Cuáles son las dimensiones del terreno? 

Situación 2

 En el área verde de un barrio hay una cancha de forma rectangular precisa para jugar vóley. En cumplimiento de la prohibición de practicar deportes grupales, será delimitada con cinta de advertencia. Se averiguó que el área de la cancha es 280 m2 y que su largo mide 6 metros más que su ancho. ¿Cuánto debe medir, como mínimo la cinta, para delimitar todo el contorno? 

Situación 3

 El municipio, actualmente a cargo del parque donde se solucionó el conflicto social, planea habilitar una ciclovía de ancho uniforme en el contorno del parque rectangular de 50 m de largo y 34 m de ancho. Se estima que el área de la ciclovía será 540 m2. ¿Cuál será el ancho de dicha ciclovía? 

Situación 4

 Compra de arbolitos Una empresa que practica la responsabilidad social, destinó S/ 4800 para la compra de cierta cantidad de arbolitos a ser sembrados en todos los parques del distrito donde efectúa sus actividades. En la compra, dicha empresa consiguió una oferta, pagando 2 soles menos por cada arbolito, lo que hizo que se compraran 200 arbolitos más con la misma cantidad de dinero. ¿Cuántos arbolitos se logró comprar? 

Situación 5

La losa deportiva de mi comunidad Una organización vecinal propietaria de un terreno dispone la construcción de una losa deportiva de concreto de forma rectangular rodeada por una vereda. Deciden que la losa deportiva sea de 12 m de ancho y 20 m de largo, y que el ancho de la vereda sea el mismo en todos los lados, siendo su área 228 m2. ¿Cuál será la medida del ancho de la vereda? ¿Cuál será el área del terreno donde se construirá la losa?

SEMANA 25

 DÍA 3 

A partir de la situación responde los siguientes retos (puedes responder de manera escrita u oral, grabando un audio): 

Situación 1 

Participando en la inauguración del parque Un parque remodelado ha organizado diversas actividades de inauguración. La familia Calsín desea participar en la mayoría de las actividades por lo que sus integrantes elaboraron un cuadro para registrar qué días pueden participar según sus edades:

a. ¿Quién pudo participar más días?

Ruth

 b. ¿Quién pudo participar menos días?

William

Situación 2

 Se tiene un presupuesto de S/ 30 000 para comprar semillas de dos tipos de pastos para la ganadería. El pasto kikuyo cuesta S/ 70 el kilogramo de semillas y el raigrás S/ 40 el kilogramo. Si bien el kikuyo es muy agradable al ganado, se restringe su uso para evitar que invada cultivos nativos. 

• ¿Cuántos kilogramos de semilla se pueden comprar, como máximo, del tipo kikuyo, para que la cantidad de raigrás sea el doble que la de kikuyo?

.:. Se puede comprar como máximo 200Kg de kikuyo.

Situación 3 

Se desea construir un área recreativa con juegos para los niños, sabiendo que el largo de terreno mide 10 m más que el ancho.

• ¿Qué medidas, como mínimo, deben tener los lados del terreno sabiendo, que por lo menos, se utilizarán 336 m2?

.:.El terreno debe tener como mínimo de largo 24m y de ancho 14m. 

DÍA 4

Situación 1

 Con la finalidad de brindar un mejor servicio educativo a sus estudiantes, una institución educativa compra un lote de computadoras por un monto total de S/ 48 000. Si hubiera conseguido cada computadora en S/ 200 menos, hubieran comprado 20 unidades más con la misma cantidad de dinero. ¿Cuántas computadoras logró comprar la institución educativa? 

.:. La I.E.compró 60 computadores

Situación 2

 Debido a la gran cantidad de turistas que asistieron el año pasado al festival de la Vendimia (Ica) y debido al distanciamiento social decretado por el gobierno, el alcalde ha decidido ampliar en 3 m el ancho y 2 m el largo la zona rectangular desde donde el público observa el pisado de uvas. Así, el área de dicha zona se duplicará respecto a la original. Calcula el área original de la zona si el largo mide 3 m más que el ancho. 

Situación 3

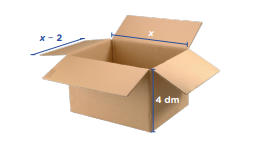
 Una compañía de alimentos necesita cajas con volumen igual a 32 dm3 para conservar sus productos. Sus características se muestran en la figura. Determina cuánto mide el largo de la caja

.:.El largo de la caja es de 4cm       

Situación 4

 Luis debe preparar su terreno cuadrangular para sembrar hortalizas y cercarlo con alambre. El costo por preparar el terreno es de S/ 10 por metro cuadrado y la cerca tiene un costo de S/ 5 el metro lineal. Determina el perímetro del terreno si el costo por prepararlo y cercarlo asciende a S/ 1200

Reemplazamos : 

Perímetro 4x=4(10)=40m

.:.El perimetro del terreno es de 40m

Situación 5 

Con la finalidad de evitar conflictos vecinales, un ingeniero hará delimitar el terreno rectangular de una asociación de vivienda que tiene 450 m de perímetro. • Calcula las dimensiones del terreno si el área delimitada debe ser al menos 3150 m2. 

.:. la dimensión del terreno de Largo es de 210m y de ancho es 15m

SEMANA 26

DÍA 3

•¿Con cuál de estos tres estudiantes te identificas? ¿Por qué?

Con la del segundo estudiante porque también se me complico plantear una ecuación

•¿Qué lección nos da la experiencia del estudiante 3?

Que si tenemos mucha dificultad para entender las situaciones de matemática pedir ayuda a tu docente o compañeros o puede ser ambos.

•¿Cómo te fue aquella vez?

todo bien

•¿Lograste comprender de qué trataba la situación?

si logre entender.

•¿Supiste plantear la situación haciendo uso del lenguaje algebraico, es decir, a través de una ecuación?

si

•¿Cómo supiste que se tenía que plantear una ecuación? 

porque hay valores desconocidos.

•¿Consideras que la situación propuesta ayuda a evitar los conflictos territoriales? 

Si ayuda porque administran las áreas verdes para su mantenimiento y preservación.

DÍA 4

1.¿Qué situación o situaciones necesitaron mayor esfuerzo de tu parte para resolverlas?

Plantear.

2.¿Qué medidas tomaste para superarlas?

Videos.

3.¿Tienes un espacio en casa para continuar con tus actividades de la estrategia Aprendo en casa? De no contar aún con él, te sugerimos habilitar un espacio cómodo, por más

pequeño que sea, siempre limpio y ventilado.

Si.

4.Es importante tener en cuenta los pasos de George Polya para resolver problemas. Describe brevemente, ¿en qué consiste cada paso? 

Plantear todos los datos y finalmente resolver

SEMANA 27    

        DÍA 3

       

Empleamos números racionales en diversas situaciones

1.¿Cómo podemos representar y operar las cantidades grandes y pequeñas mencionadas en la descripción de la situación? 

Se puede representar y operar las cantidades grandes y pequeñas convirtiéndolas a notación científica. 

2.¿De qué manera podemos enfrentar esta problemática de salud? 

Cumpliendo las medidas de seguridad dichas por el estado.

3.La pérdida de dinero que registran los países por la pandemia, ¿está justificada? Argumenta tu respuesta

Si, ya que es un gasto por el cuidado de la salud de sus ciudadanos. 

•Pedro vende mascarillas al por mayor, siguiendo todos los protocolos de seguridad. Cada día se asegura de disponer para la venta la misma cantidad de mascarillas e intenta vender la mayor parte posible de esa cantidad. Observa cómo le fue con su venta de lunes a viernes:

¿Qué fracción de las mascarillas pudo haber vendido Pedro los días miércoles y viernes? Argumenta tu respuesta.

DÍA 4

1-Como se sabe, en los espacios públicos de muchos países se han trazado una serie de circunferencias en el piso para que las personas se ubiquen manteniendo el distanciamiento social. Por ese motivo, y respetando los protocolos de seguridad, se encarga a terceros la labor de trazar circunferencias de distanciamiento en las veredas próximas al ingreso de locales comerciales. Supón que te encargan apoyar en esta labor haciendo un plano de cómo quedaría el trazado de circunferencias sobre un papel. Por ejemplo, 

¿cómo quedaría el trazado y representado a escala, una de las circunferencias con √2 cm de radio?

¿Y si la representación tuviera √3 cm de radio?

2-El papá de Jorge fue diagnosticado como paciente de COVID-19 con síntomas leves. En el hospital le recomendaron aislamiento en casa y el monitoreo de sus valores de saturación de oxígeno en la sangre 3 veces al día. En la siguiente tabla se registró la información:

•Representa gráficamente, la oscilación de los valores de saturación de oxígeno por día.

•Representa gráficamente, la oscilación de los valores de saturación de oxígeno durante su monitoreo en casa.

•Representa gráficamente, la oscilación de los valores de saturación de oxígeno los días lunes y miércoles

•¿Por qué razón no se registran datos los días jueves y viernes?

En este caso, el nivel de saturación de oxígeno en la sangre es recomendable que se encuentre entre 95% y el 100%. Por debajo de un 90% se podría producir lo que se llama hipoxemia con lo que esa persona tiene dificultad a la hora de respirar. Como se presento en la primera tabla el dia jueves a las 16h presenta un 91% y mas bajo seria peligroso.

3-El reloj que se muestra está programado para dar la temperatura ambiente cada dos horas. Luis ha estado anotando las temperaturas desde la madrugada, registrándolas en la siguiente tabla:

a. ¿Cuál es el promedio de la temperatura entre las 08 h 00 y a las 10 h 00? 

b. ¿Entre qué horas se produjo el mayor aumento de temperatura? 

El mayor aumento o incremento de temperatura se registró entre las 06:00 y 8:00 horas con 8.1ºC. 

c. Se sabe que al mediodía la temperatura es el doble de la que se registra a las 06 h 00, ¿Cuál es la temperatura al mediodía?

18,5ºCx2=37ºC La temperatura al medio día es 

SEMANA 28

          

           DÍA 3      

•En los primeros meses de la cuarentena decretada en nuestro país, entre otras medidas de seguridad, se decretó el toque de queda. El gobierno anunciaba que, durante el toque de queda, los vehículos deberán transitar a una velocidad no mayor de 30 km/h.

1. ¿Qué significa ir a una velocidad de 30 km/h?

Significa que el límite máximo de la velocidad de 30 kilómetros por hora. Es decir, cada hora recorre 30 kilómetros; por que la velocidad es constante.

2. ¿Cuántos metros de recorrido implica ir a esa velocidad durante 12 s?

3. ¿Cuántos minutos tardaría un vehículo a esa velocidad en recorrer 50 000 m?

4. Una persona antes de la pandemia llegaba a su casa en 50 minutos y ahora se demora dos horas y media en llegar a su domicilio, ¿a qué velocidad, en metros por segundo, transitaba antes de la pandemia?

5. Si una persona antes de la pandemia llegaba a su casa en 50 minutos y ahora se demora dos horas y media en llegar a su domicilio, ¿a cuántos kilómetros de su domicilio queda su centro laboral?

situación 2

Un hospital de emergencias concretó una reciente recarga de 10 mil metros cúbicos de oxígeno medicinal, el cual permitirá garantizar de manera oportuna la dotación de oxígeno a pacientes de COVID-19. Los balones de 6 metros cúbicos alcanzan para 12 horas de oxígeno, vienen con la válvula y el regulador listo para ser instalado en la mascarilla.

 • El hospital cuenta con 8 salas para pacientes de COVID-19 y se distribuye el oxígeno en la misma cantidad. A cada paciente se le administrará 2 m3 durante 5 días, ¿cuántos pacientes se beneficiarán con el oxígeno en cada una de las salas? 

• Si en una sala 25 pacientes son dados de alta y se distribuye el oxígeno en la misma cantidad, ¿qué cantidad de oxígeno le correspondería a cada paciente durante 5 días?  

       DÍA 4       

Situación 1

 Bonos a la familia La situación generada por el COVID-19 impulsó al Gobierno a otorgar ayuda económica directa a las familias en situación de pobreza y vulnerabilidad que vieron interrumpidos sus ingresos. Explicaremos con detalle cuáles son los diferentes bonos de 760 soles otorgados por el Gobierno hasta la fecha:

¿A cuánto asciende el monto abonado por el Gobierno Peruano?

2-Juan adquirió mascarillas de tela y le informaron que obedecían lo señalado por la R.M. 135-2020-MINSA2, que norma las especificaciones técnicas para la confección de mascarillas faciales textiles de uso comunitario.

¿Cuál tipo de mascarillas será de óptima protección ante el coronavirus? Argumenta tu respuesta.

SEMANA 29

DÍA 3

•¿Con qué frecuencia las personas de nuestro entorno realizan actividad física, de acuerdo con las recomendaciones de la OMS? 

Los niños y adolescentes de entre 5 y 17 años dedican al menos 60 minutos al día a realizar ejercicio físico de moderado a vigoroso.

•¿Cómo contribuye la actividad física a nuestra salud? 

Bueno la actividad física contribuye a evitar las enfermedades no transmisibles como el cáncer y la diabetes.

•¿Qué podríamos hacer para incentivar la actividad física de los integrantes de nuestra familia?

Primero cada miembro de la familia debe reconocer la importancia de las actividades físicas para vivir saludablemente luego realizar pequeñas actividades como salir a respirar aire puro , jugar con la pelota , etc. 

1-También en nuestro entorno, percibimos que la actividad física de los adolescentes va en descenso. Preocupados por ello, en una I. E., que cuenta con 124 estudiantes, se han propuesto estudiar la frecuencia de prácticas deportivas. Para lo cual, se te ha encargado solventar las siguientes tareas:

a. ¿Cómo podríamos elegir aleatoriamente una muestra de 20 estudiantes? 

El muestreo aleatorio simple es un método de selección de n unidades sacadas de N, de tal manera que cada una de las muestras tiene la misma probabilidad de ser elegida.

b. ¿Cómo podríamos elegir sistemáticamente la muestra de 20 estudiantes en dicha institución?

DÌA 4

Situación 1

 La actividad consiste en identificar el tipo de variables relacionadas con la actividad física y recopilar datos organizándolos en tablas. La recopilación se realizará a través de una encuesta y será aplicada por ti a los integrantes de tu familia, compañeras, compañeros y otras personas que consideres conveniente. Se sugiere que apliques la encuesta por lo menos a 20 personas. Las preguntas que se muestran a continuación se presentan como propuesta, si consideras conveniente, puedes agregar otras o cambiarlas. A partir de estas preguntas, debes elaborar una encuesta en físico o de manera virtual. Las respuestas a estas preguntas se deben organizar en tablas apropiadas al tipo de variable. Preguntas sugeridas para la encuesta: 

 8. ¿Cuáles son las razones principales por las cuales haces ejercicio?

a. Por salud (X) 

b. Porque lo disfruto ( )

 c. Por moda ( )

 d. Otra:  ………………………………………………………………

2-Walter, un joven estudiante de 5.° grado de secundaria, aplica una encuesta a 15 personas de su entorno. Ahora, presenta conclusiones basadas en sus resultados:

a) ¿Cuáles pudieron haber sido las preguntas que hizo Walter para obtener estos resultados? 

¿Con qué frecuencia realizas ejercicios? 

a) Diario 

b) Interdiario 

c) Semanalmente 

d) Nunca

b) ¿Cuál es la variable en estudio para cada pregunta identificada? 

Variable: Edad (cuantitativa)

Variable: frecuencia realizas ejercicios (cualitativa)

c) ¿Qué procedimientos deberá realizar para dar las conclusiones? 

Debemos hallar las medidas de tendencia central y medidas de dispersión para ver la homogeneidad de los datos.

SEMANA 30

DÌA 3

Situación 1

 La actividad física de un grupo de estudiantes Se aplicó una encuesta a 40 estudiantes de una I. E. que participan de la estrategia Aprendo en casa para recabar información relacionada con las actividades físicas que desarrollan.

A partir de los datos, realiza los siguientes retos para esta institución educativa:

a) Identificar la población, la muestra y la variable estadística.

POBLACIÓN: alumnos de la I.E.

 MUESTRA: 40 estudiantes de la I.E 

VARIABLE: Tenemos las siguientes tipos de variables en la encuesta

 1ERA PREGUNTA: la variable es la EDAD (Variable cuantitativa)

 2DA PREGUNTA: la variable es el tiempo (Variable cuantitativa) 

3 ERA PREGUNTA: la variable es el tipo de actividad física (Variablre cualitativa)

 4 TA PREGUNTA: la variable es el tipo de ejercicios físicos (Variablre cualitativa)

b) Elaborar la tabla de frecuencias, determinando el recorrido, el número de intervalos y la amplitud de cada intervalo. 

c) Analizar la información obtenida. 

Se puede observar que la edad más frecuente de los estudiantes se encuentra en [12-14 [, el 10%

de los estudiantes tienen 6 o 7 años, también se puede observar El porcentaje de estudiantes de edad [8-10 [y [14-16] es el mismo. d) Representar gráficamente la información y realizar su interpretación. 

Situación 2

 Tomando como referencia la pregunta de la encuesta relacionada con la variable “tipo de ejercicio físico y, las edades de la situación anterior, Alexis elabora la siguiente tabla de frecuencias: 

Se solicita ayudar a Alexis a completar los datos que faltan en la tabla; luego, representar gráficamente la información y realizar su interpretación.

Podemos interpretar que de los estudiantes encuestados el 32% hacen ejercicios de velocidad, el 38% hacen ejercicios de resistencia y el 30% de los estudiantes realizan ejercicios de flexibilidad. 

Podemos interpretar la cantidad de participantes según el intervalo de edad, que participa en cierto tipo de actividad física.

DÌA 4

Situación 1

 La actividad física de un grupo de estudiantes A partir de la tabla de frecuencias que elaboraste para la situación 1, inciso b), calcula las medidas de tendencia central: media aritmética, moda y mediana e interpreta.

2.- La siguiente tabla muestra los datos de una encuesta realizada a 18 personas entre familiares y vecinos que practican ejercicio físico para mantener una buena salud. 

SEMANA 31

DÍA 3

1. ¿De qué manera podrías proponer un plan familiar de gestión de riesgos ante los sismos?

 Hablando con mi familia, y elaborar un plan de cuidado ante un desastre de sismo.  

2. ¿Qué acciones pondrías en práctica para el antes, durante y después de un sismo? 

Antes de un sismo: 

-Anticipar al peligro identificando los sitios de alto riesgo de la casa o el lugar de trabajo.

 - Definir de forma participativa el plan de emergencia en caso de un sismo, así como las rutas para la evacuación de la vivienda.

Durante de un sismo:

 - Mantener la calma.

 - Buscar un sitio seguro para protegerse.

Después de un sismo: 

- Reunirse con los familiares en un lugar seguro.

 - Si se está en capacidad de hacerlo, aplica los primeros auxilios a las personas lesionadas. 

Situación 1

 José ha interiorizado la importancia de contar con carteles y señales de seguridad para colocar en su vivienda para indicar los lugares apropiados para ubicarse él y su familia. Para su elaboración, toma como referencia la Tabla C1 donde se registran los formatos de las señales y carteles según la distancia máxima de visualización 

TABLA C1 - FORMATOS DE LAS SEÑALES Y CARTELES SEGÚN LA DISTANCIA MÁXIMA DE VISUALIZACIÓN.

b. Elabora 4 o más carteles o señales de seguridad variados, respetando los aspectos técnicos en cuanto al tamaño y forma.

c. Calcula el área y perímetro de los carteles o señales de seguridad que van a elaborar

DÍA 4

1. ¿Cuáles son las características de infraestructura de tu vivienda? 

Material de concreto, puertas de madera, casa de dos pisos. 

2. ¿Sabes qué lugares de tu casa son los más seguros y los más peligrosos?

 Las zonas seguras son las columnas y peligrosa donde ventanas grandes. 

3. Dibuja un plano de tu casa, a una escala conveniente, de modo que se identifiquen allí las zonas seguras y de evacuación hacia la vía pública

Situación 2

 El siguiente plano muestra una leyenda de escala 1:75. Tomando la medida con una regla, las dimensiones de la sala que se obtienen son:

 Largo: 7 cm Ancho: 5,2 cm 

¿Cuáles son las dimensiones reales de dicho ambiente y cuál su área? 

Situación 3

 La estudiante Gladys Calsín realizó el plano de su localidad, en dicho plano se muestra la escala. Ella nos comenta que la señal de punto de reunión la tenían pintada y ubicada en el patio de su Institución Educativa; como en esta época de emergencia sanitaria la institución está cerrada y, además, al trasladarse deben hacerlo de manera ordenada y con mascarillas.

a. en qué lugar propones que debería estar ubicado el cartel de “Punto de reunión”. Justifica tu respuesta.

En la Plaza 8 de Octubre porque es un espacio abierto libre donde resistirá el derrumbe de edificios o comercios.

b. De producirse un sismo, ¿cuántos metros deben desplazarse los integrantes de la familia Calsín al “Punto de reunión”?

𝐹𝑎𝑚𝑖𝑙𝑖𝑎 𝐶𝑎𝑙𝑠𝑖𝑛 = 17(3𝑚) + 1𝑚 

𝐹𝑎𝑚𝑖𝑙𝑖𝑎 𝐶𝑎𝑙𝑠𝑖𝑛 = 51𝑚 + 1𝑚 

𝐹𝑎𝑚𝑖𝑙𝑖𝑎 𝐶𝑎𝑙𝑠𝑖𝑛 = 52

c. Y, ¿cuántos metros la familia López?

𝐹𝑎𝑚𝑖𝑙𝑖𝑎 𝐿ó𝑝𝑒𝑧 = 24(3𝑚) 

𝐹𝑎𝑚𝑖𝑙𝑖𝑎 𝐿ó𝑝𝑒𝑧 =72m

SEMANA 32

DÍA 3

Situación 1

 Respecto a la ruta de evacuación óptima frente a la posibilidad de un sismo, Junior y su familia optaron por ir hacia la canchita, tomando con precaución el recorrido en línea recta por la avenida que los une.

¿A qué distancia real está la canchita de la casa?

Situación 2:

 Karina se pregunta: si ocurriera un sismo cuando estoy en la biblioteca municipal, que se encuentra a 200 m a la derecha y 100 m al norte de mi casa, y debo salir para dirigirme al parque que se encuentra a 200 m a la derecha y 200 m al norte de la biblioteca, ¿cuál será la distancia que recorrería para poder unirme con mis familiares en aquel parque?

Situación 3:

 Identifica las zonas seguras en el interior de tu casa. Haz lo mismo en el exterior, identifica dos o tres lugares hacia donde podrían evacuar tú y tu familia, y ubícalos en un sistema de coordenadas tal que:

 a. Estimes las distancias entre estos lugares y tu casa. 

b. Estimes la superficie real de aquellas zonas seguras para emitir un informe respecto al aforo de personas.

DÌA 4

-El siguiente documento evidencia el préstamo de S/ 2500 que otorga José Balta a Enrique Cárdenas, bajo los términos y condiciones siguientes:

Se quiere saber si el interés alcanzará a José Balta para reponer dos mochilas de emergencia de 391 soles cada una. Justifica tu respuesta.

SITUACION 2

-Luego de un sismo reciente, la casa de la familia Cárdenas quedó dañada como muestra la imagen.Para reparar y reforzar el muro se necesita levantar una columna en el extremo que da a la calle y colocar una viga horizontal, el costo aproximado es de S/ 2000. Para financiarlo solicitan un préstamo por dicho monto.

La entidad “El Emprendedor” ofrece un préstamo de S/ 2000 por un periodo de 18 meses, a una tasa de interés del 20 % anual, capitalizable semestralmente. 

SEMANA 33

DÍA 3

a. ¿De qué manera organizarías tu tiempo para desarrollar las actividades propuestas?

En horario de clases virtuales, realización de tareas, deberes de casa, recreación.

b. ¿Qué otras propuestas concretas darías para prevenir la violencia contra las niñas y las mujeres?

Generar conciencia en las personas, hablando con ellas(os) o mediante afiches.

Situación 1

Actividades en familia

Con la finalidad de usar el tiempo libre para compartir actividades de creación y recreación, 4 integrantes de una familia, deciden elaborar un álbum de fotografías componiendo historias breves y amigables, para ello se han propuesto que, de manera simultánea, en 2 minutos, cada integrante elaborará una página del álbum

a. Determinar el modelo, la cantidad de las páginas que han elaborado los 4 integrantes de la familia en términos del tiempo.  n= 𝟐𝒕

b. Calcular la cantidad de páginas del álbum que elaborarán los 4 integrantes de la familia, en 2 horas. 

2h= 𝟏𝟐𝟎𝒎𝒊𝒏 n= 𝟐𝒕 n= 𝟐(𝟏𝟐𝟎) n= 𝟐𝟒𝟎

c. Determinar el tiempo que emplearán para elaborar 80 páginas del álbum.

n= 𝟐𝒕  8𝟎 = 𝟐𝒕  80/2= 𝒕 4𝟎 = 𝒕

 d. Realizar la representación gráfica e interpretarla. 

 

Situación 2

Leyenda en el Dakar

Fernanda Kanno cambió su vida por los autos. Desde el 2018, corre en el Rally Dakar y en el 2019 se convirtió en la primera peruana en culminar la carrera. En una entrevista, manifestó lo siguiente: “Siempre es bonito lograr algo, sobre todo si eso puede inspirar a otros a hacer lo mismo. Las mujeres queremos que se nos trate igual que a los hombres, entonces separar las cosas y darnos mérito por el hecho de ser mujeres no es igualdad, sino un trato especial. Quiero que todas las personas entiendan que pueden hacer lo mismo que yo y vivir como sueñan”. Se sabe que en sus competencias debe correr a 180 km por hora en promedio. 

 a. ¿Qué modelo lineal representa la situación planteada? 

d= 𝟏𝟖𝟎𝒕

b. ¿Cuántas horas deberá conducir Fernanda para recorrer 1800 km?

Situación 3

Los miembros de una familia se distraen haciendo secuencias de construcciones con cubitos y ya han armado hasta la construcción 3, tal como se muestra: 

b. Expresa el comportamiento del número de cubitos a través de una función lineal y grafícala.

DÍA 4

Situación 1

Liliana y su familia están evaluando contratar un nuevo servicio de telefonía para cubrir las necesidades de comunicación en su casa. Hasta ahora tenían un consumo mensual de 100 minutos, pero con la llegada de un familiar, se estima que el consumo mensual ascienda a 300 minutos. Una empresa de telefonía les ofrece los siguientes planes:

Plan A: pago fijo mensual de S/ 20, y por cada minuto de llamada el costo es de S/ 0,20.

Plan B: no hay pago fijo mensual, pero por cada minuto de llamada el costo es de S/ 0,30. 

Situación 2

La familia Barreda se dedica a la venta de productos de limpieza, ferreteros y otros. Frente a la demanda de equipos de protección, planean implementar la venta de mascarillas. En el almuerzo del domingo se reúne la familia para decidir entre las propuestas de dos proveedores:

Proveedor 1: ofrece las mascarillas a 1,20 soles cada una.

Proveedor 2: ofrece a 1 sol cada una más un costo de envío de 3 soles.